跳转至

网络攻击的特征

数据集介绍

KDD Cup

  • 国际知识发现和数据挖掘竞赛1

  • KDD Cup 1999年主题：入侵检测2

    • 攻击分为四类：probing（扫描探测）、DoS（拒绝服务）、U2R（未授权本地超级用户访问）、R2L（未授权远程访问）
    • DoS攻击又分为六种：Back、Land、Neptune、Pod、Smurf、Teardrop
    • 拥有大约4GB的TCP dump数据，500万条连接数据，是累计七周的网络流量
    基于kNN的入侵检测分类方法
    1. 计算样本与训练集各个样本的距离
    2. 找到最近的k个邻居
    3. 如果超过k/2是Ak类，则认为样本集属于Ak类
    4. 否则选最大的Ap作为类别
    5. 都不满足，则为新类型

分析方法

降维

降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。

优点

  1. 数据集更易使用
  2. 降低计算开销
  3. 去除噪声
  4. 结果更易理解

降维算法

奇异值分解(SVD)、主成分分析(PCA)、因子分析(FA)、独立成分分析(ICA)都是常见的降维算法

  • PCA与FA的对比

    PCA FA
    \(c=w_1(Y_1)+w_2(Y_2)+w_3(Y_3)+w_4(Y_4)\) \(Y_1=b_1*F+u_1\)
    \(Y_2=b_2*F+u_2\)
    \(Y_3=b_3*F+u_3\)
    \(Y_4=b_4*F+u_4\)

PCA

主成分分析在做什么

通过将原始变量转换为原始变量的线性组合(主成分)，在保留主要信息的基础上，达到简化和降维的目的

  • 特点

    • 主成分是原始变量的线性组合
    • 主成分的数量相对于原始数量更少
    • 主成分保留了原始变量的大部分信息
    • 主成分之间相互独立

  • PCA 的主要思想是将 \(n\) 维特征映射到 \(k\) 维上，这 \(k\) 维是全新的正交特征，也被称为主成分，是在原有 \(n\) 维特征的基础上重新构造出来的 \(k\) 维特征 。

  • 算法实现(基于特征值分解协方差矩阵，数据集 \(X=\{x_1,x_2,\cdots ,x_n \}\) )

    1. 去平均值(即去中心化)，即每一位特征减去各自的平均值。
    2. 计算协方差矩阵 \(\dfrac{1}{n}XX^T\)
    3. 用特征值分解方法求协方差矩阵 \(\dfrac{1}{n}XX^T\) 的特征值与特征向量
    4. 对特征值从大到小排序，选择其中最大的 \(k\) 个。然后将其对应的 \(k\) 个特征向量分别作为行向量组成特征向量矩阵 \(P\) 。
    5. 将数据转换到 \(k\) 个特征向量构建的新空间中， 即 \(Y=PX\)

  • 实验：IRIS数据集(3种花，150条数据，特征为花瓣/花萼的长度和宽度)3

FA

因子分析在做什么

通过研究众多变量之间的内部依赖关系，探求观测数据的基本结构，并用少数几个假想变量因子来表示原始数据

  • 特点

    • 因子个数远远少于原始变量个数
    • 因子并非原始变量的简单取舍，而是一种新的综合
    • 因子之间没有线性关系
    • 因子具有明确解释性，可以最大限度地发挥专业分析的作用。这个与主成分分析做对比，主成分分析只要求方差大

  • 每个原始变量存在一个内部的“隐变量”

  • 实验：bfi2010(25个有关个性的问题，内部与5个隐藏特征有关)4

    • 这五个隐藏特征又称为“大 5 人格模型”

网络攻击的模型解释

随着模型越来越复杂，模型的透明性在下降。我们需要一个方法来理解这些模型

全局角度

  • 二分类/0-1分类：Logistic Regression(LR)

    • 使用一个线性拟合函数 \(f(x)\) ，在外层套上一个Sigmold函数，其表达式如下
    \[ P=\frac{1}{1+\mathrm{e}^{-(a+bX)} } \quad (x=a+bX) \]
    • 解优化方程，找出使损失函数(描述预测的值与真实值差距的函数)值最小的 \(w\) 值，其表达式如下
    \[ \begin{align} J(\theta )&=-\dfrac{1}{m} \sum_{i=1}^{m} [y^{(i)}\log (h_\theta (x^{(i)}))+(1-y^{(i)})\log (1-h_\theta (x^{(i)}))] \\ 其中， f_{w,b}(x)&=\sigma (\sum_{i}^{}w_ix_i+b ) \\ \sigma (z)&=\frac{1}{1+ \mathrm{e}^{-z}} \end{align} \]

  • LightGBM贡献度

    • LightGBM 是基于决策树的 boosting 算法

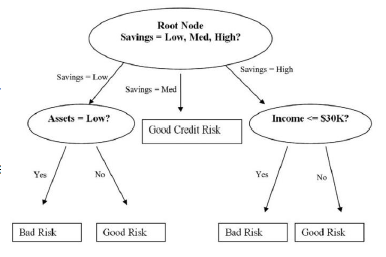
    attack-feature-1
    关于评价借款风险高低的决策树

    • boosting 算法使用多个模型组合来预测

      Ensemble methods

      集成算法的核心就是训练多个弱分类器，将多个弱分类器集合在一起，组成一个强分类器

      • 对抗过拟合：Bagging(Bootstrap Aggregating)，一般用于强分类模型
        • 可减少模型的方差
      • Boosting，一般用于弱分类模型
        • 每一个新的模型是从上一个模型的分类错误的结果中进行学习
      • Stacking，训练一个新的模型来合并每一个模型的预测值

      对于Bagging/Boosting的比较

      单个模型 Bagging Boosting
      分类器数量 单一分类器 多个分类器 多个分类器
      训练集使用 使用整个训练集 会对于每一个模型在训练集中进行随机抽样 增加上一个模型误分类样本的权重
      训练情况 只训练一个模型 可平行训练 按照顺序训练
      权重使用 直接使用权重 平均权重 计算每一个模型的权重

局部角度

给一张图片 \(I_0\)，对应的分类是 \(c\)，有一个模型给出图片 \(I_0\) 的概率值是 \(S_c(I)\) ，我们想要衡量 \(I_0\) 的某个像素点对分类器 \(S_c(I)\) 的影响。

\[ \begin{align} S_c(I) \begin{cases} = w_c^TI+b_c \quad &S_c(I)是一个线性模型 \\ \approx w^TI+b \quad &S_c(I)是一个复杂模型 \end{cases} \end{align} \]
  • 对于复杂模型，其中的 \(W\) 就是模型 \(S_c(I)\) 对 \(I\) 的导数
  • 最终要计算出 \(W\) 的值

存在的问题

Saliency 会出现梯度饱和的现象，也就是一些重要的特征可能梯度计算出来是 0。

使用简单的模型在局部来拟合复杂的函数，只能对某个样本进行解释。

全称SHapley Additive exPlantions，是用来分配收益的一种计算方式

  • 我们可以计算每个人加入前后给整个团队带来的收益，他能带给团队的收益就是他能分配到的收益；具体来说，是计算所有 player 加入情况下的边际收益，然后求平均值，就可以得到 Shapley Value
\[ \phi _i(v)=\dfrac{1}{|N|!}\sum_{R}^{} [v(P_i^R \cup \{i\})-v(P_i^R)] \]
  • \(N!\) 表示所有合作的可能性，\(\phi _i(S)=v(S \cup \{i\})-v(S)\) 表示 \(i\) 加入集合 \(S\) 后的边际贡献
  • 计算特征的重要度
    • 我们计算这个模型有 feature \(i\) 和没有 feature \(i\) 时候的值
  • 处理特征缺失——用特征在整个数据集上的期望值替代

  1. 官方网站 https://www.kdd.org/kdd-cup ↩

  2. 数据集下载 http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html ↩

  3. http://www.lac.inpe.br/~rafael.santos/Docs/CAP394/WholeStory-Iris.html ↩

  4. https://vincentarelbundock.github.io/Rdatasets/doc/psych/bfi.html ↩

  5. Simonyan K, Vedaldi A, Zisserman A. Deep inside convolutional networks: Visualising image classification models and saliency maps[J]. arXiv preprint arXiv:1312.6034, 2013. ↩

  6. Ribeiro, Marco Tulio, Sameer Singh, and Carlos Guestrin . “Why should I trust you?: Explaining the predictions of any classifier.” Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. ACM (2016). ↩

  7. Lundberg SM, Lee SI (2017), “Consistent feature attribution for tree ensembles”, presented at the 2017 ICML Workshop on Human Interpretability in Machine Learning (WHI 2017), Sydney, NSW, Australia (https://arxiv.org/abs/1706.06060) ↩

  8. Lundberg SM, Lee SI (2017), “ A Unified Approach to Interpreting Model Predictions ”, Neural Information Processing Systems (NIPS) 2017 (https://arxiv.org/abs/1705.07874) ↩

  9. Lundberg, Scott M., et al. "Explainable machine learning predictions for the prevention of hypoxaemia during surgery." Nature Biomedical Engineering 2.10 (2018):749. ↩