数据的表示与运算

数制与编码

进位计数制及相互转换

基数: 每个数码位所用到的不同符号的个数，r进制的基数为r

常见进制使用的符号

二进制：0、1（计算机的选择），用b（binary）表示
八进制：0、1、2、3、4、5、6、7
十进制：0、1、2、3、4、5、6、7、8、9，用D（decimal）表示
十六进制：0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F，用H（hexadecimal）表示，也可以用0x作为前缀

为什么计算机选择了二进制

可使用两个稳定状态的物理器件表示
0、1正好对应逻辑假、真，方便实现逻辑运算
可以很方便地使用逻辑门电路实现算术运算

其他进制转十进制二进制与八进制、十六进制互转十进制转任意进制

\[ \overline{K_nK_{n-1}\cdots K_2K_1K_0K_{-1}K_{-2}\cdots K_{-m}} =K_nr^n+K_{n-1}r^{n-1}+\cdots+K_2r^2+K_1r^1+K_0r^0+K_{-1}r^{-1}+K_{-2}r^{-2}+\cdots +K_{-m}r^{-m} \]

二进制转换为八进制、十六进制八进制、十六进制转换为二进制

在二进制转八进制时，3位一组，每组转换成对应的八进制符号

Text Only

1111000010.01101   二进制
     ↓
001 111 000 010.011 010
 1   7   0   2 . 3   2   八进制

在二进制转十六进制时，4位一组，每组转换成对应的十六进制符号

Text Only

1111000010.01101   二进制
     ↓
0011 1100 0010.0110 1000
  3    C    2 . 6    8    十六进制

小数点前在二进制最前面补0凑齐组，小数点后在最后面补0凑齐组

在八进制转二进制时，每位八进制对应3位二进制

Text Only

  1  7   2 . 3   2   八进制
     ↓
001 110 010.010 000   二进制

在十六进制转二进制时，每位十六进制对应4位二进制

Text Only

  A    E   8    6  . 1  十六进制
   ↓
1010 1110 1000 0110.0001 二进制

整数小数

除基取余法，将整数部分不断除以基数r，得到从低位到高位的余数

Text Only

(75.3)10 整数部分为75
75 / 2 = 37 ... 1
37 / 2 = 18 ... 1
18 / 2 = 9  ... 0
9  / 2 = 4  ... 1
4  / 2 = 2  ... 0
2  / 2 = 1  ... 0
1  / 2 = 1  ... 1   ↑
(75)10=(1001011)2

乘基取整法，将小数部分不断乘以基数r，得到从高位到低位的余数

Text Only

(75.3)10 整数部分为75
75 / 2 = 37 ... 1
37 / 2 = 18 ... 1
18 / 2 = 9  ... 0
9  / 2 = 4  ... 1
4  / 2 = 2  ... 0
2  / 2 = 1  ... 0
1  / 2 = 1  ... 1   ↑
(75)10=(1001011)2

真值和机器数

真值: 符合人类习惯的数字，实际带正负号
机器数: 数字实际存在机器里的形式，把正负号数字化了

字符和字符串

英文字符在计算机内的表示：ASCII码（8位）
- 可印刷字符：32~126，其余为控制、通信字符
- 数字：48（0011 0000）~57（0011 1001）
- 大写字母：65（0100 0001）~90（0101 1010）
- 小写字母：97（0110 0001）~122（0111 1010）
- 后四位恰好是8421码
中文字符在计算机内的表示
- GB2312-80：汉字+各种符号共7445个
- GB18030-2005：变长字节编码，共收录汉字70244个
- 区位码：94个区，每区94个位置
- 国标码：区位码+2020H，防止信息交换时与“控制/通信字符”冲突
- 汉字内码：国标码+8080H，防止信息交换时与ASCII码冲突

字符串的存储

按字节编址，s="abc" 的存储

Text Only

+------+-------+-------+-------+--------+-------
|      |  61H  |  62H  |  63H  |   00H  |  ... 
+------+-------+-------+-------+--------+-------
           a        b      c        \0（字符串结束符）

按字节编址，s="abc啊" 的存储

大端模式小端模式

数据的最高有效字节存放在低地址单元中。

Text Only

+------+-------+-------+-------+-------+--------+--------+-------
|      |  61H  |  62H  |  63H  |   B0H |  A1H   |   00H  |  ... 
+------+-------+-------+-------+-------+--------+--------+-------
           a        b      c           啊            \0（字符串结束符）

将数据的最高有效字节存放在高地址单元中。

Text Only

+------+------+-------+-------+-------+-------+--------+-------
|      | 61H  |  62H  |  63H  |   A1H |  B0H  |   00H  |  ...
+------+------+-------+-------+-------+-------+--------+-------
          a        b      c           啊            \0（字符串结束符）

定点数的表示和运算

定点数的表示

无符号数

计算机通用寄存器的字长决定了计算机无符号位数的上限
全部二进制位是数值位，没有符号位
最小数字全0，最大数字全1

有符号数

对有符号数而言，符号的“正”、“负”机器是无法识别的，但由于“正”、“负”恰好是两种截然不同的状态，如果用“0”表示“正”，用“1”表示负，这样符号也被数字化了，并且规定将它放在有效数字的前面，即组成了有符号数。

Text Only

+----+-----------------+
| x0 |       x         |
+----+-----------------+
 符号位     数值位

原码反码补码移码

符号位为0表示整数，符号位为1表示负数，数值位即真值的绝对值。
更便于人类理解

原码存在+0(0,0000000)和-0(1,0000000)两种表示

整数小数

表示范围：\(-(2^n-1)\le x \le 2^n-1\)

Text Only

+----+------------------+
| 符 | 2^n ...  2^1  2^0|
+----+------------------+
 用 , 隔开

表示范围：\(-(1-2^{-n})\le x \le 1-2^{-n}\)

Text Only

+----+------------------+
| 符 | 2^-1 2^-2 ...2^-n|
+----+------------------+
 用 . 隔开

符号位为0时，反码与原码相同；符号位为1时，反码为原码除符号位外各位取反。
中间状态

正数补码=原码，负数补码=反码末位+1（考虑进位）。真值0只有一种形式。
更便于计算机运算
定点整数补码1,0000000表示 \(x=2^{-7}\)
- n+1位字长表示范围 \(-2^n\le x \le 2^n-1\)
定点小数补码1.0000000表示 \(x=-1\)
- n+1位字长表示范围 \(-1\le x\le 1-2^{-n}\)

补码尾数取反，末位加一可以得到相应原码

补码符号位取反，只能表示整数，真值0只有一种。

定点整数和定点小数表示范围

码制	定点整数	定点小数	数码个数
原码	-(2^{n-1}-1)~+2-1	-(1-2^{{-(n-1)})~+(1-2})	2^n-1
反码	-(2^{n-1}-1)~+2-1	-(1-2^{{-(n-1)})~+(1-2})	2^n-1
补码	-2^{n-1}~+2-1	-1~+(1-2^{-(n-1)})	2^n
移码	-2^{n-1}~+2-1	-1~+(1-2^{-(n-1)})	2^n

定点数的运算

移位运算

算术移位
- 移位过程中符号位保持不变，对象为有符号数
- 正数：移位后的空位补0
- 负数
  - 原码：空位补0，若不产生溢出，左移相当于乘上2，右移相当于除以2
  - 补码：左移空位补0，右移空位补1
  - 反码：空位补1
逻辑移位
- 操作数作为无符号数看待
- 右移：高位补0，低位舍弃
- 左移：低位补0，高位舍弃

循环移位

Text Only

  n         32-n
+----+-----------------+
|    |                 |
+----+-----------------+
          ↓
+-----------------+----+
|                 |    |
+-----------------+----+
     32-n           n

假设是对32bit整数进行操作，有以下循环移动公式
- 循环左移：y=(val>>(N-n)) | (val << n))
- 循环右移：y=(val<<(32-n) | (val >> n))

符号扩展

将有符号数扩展到更长位数。

正数负数

将符号位0移动到最高位，其他空位补0

原码补码反码

将符号位1移动到最高位，其他空位补0

将符号位1移动到最高位，整数其他空位补1，小数其他空位补0

将符号位1移动到最高位，其他空位补1

加减运算

原码加减
加法减法
- 两个数的符号位相同，结果的符号位与两个数的符号位相同
- 两个数的符号位不同，结果的符号位与绝对值较大的数的符号位相同
减数符号取反转换为加法
补码加减（计算机常用）

\[ \begin{align*} [A+B]_补&=[A]_补+[B]_补 \\ [A-B]_补&=[A]_补-[B]_补=[A]_补+[(-B)]_补 \end{align*} \]
- 因此，只需加法器。符号位也来运算

乘除运算

乘法

原码一位乘法补码一位乘法（Booth算法）

欲计算原码表示的 \(x_sx_1x_2\cdots x_n \times y_sy_1y_2\cdots y_n\)：

乘积符号位为两数符号位异或
从乘数y的最低位开始，若其值为 1，则将x的数值位（n位）加到乘积数值位的高n位；若其值为 0，则不加。
乘积的数值位逻辑右移一位，乘数y逻辑右移一位。若上一步产生了进位，需要将进位也移动到乘积最高位。
将步骤2、3重复n次，即可得到乘积的数值位

欲计算补码表示的 \(x_sx_1x_2\cdots x_n \times y_sy_1y_2\cdots y_n\)：

采用双符号位，符号位也参与运算
乘积m的高 \((n+1)\) 位要加上 \((y_{i+1}−y_i)x\)，也即根据乘数y的最后两位来确定对乘积的操作。进位舍去。
对乘积进行算术右移一位，乘数右移一位。
将步骤2、3重复 \((n+1)\) 次，最后一次不进行右移，即可得到乘积的数值位

除法

原码补码

恢复余数法加减交替法

商的初始值为 0，余数的初始值为被除数的数值位（\(0.x_1x_2\cdots x_n\)）。由于减去除数可以改为加上除数相反数的补码，为 \([0.y_1y_2\cdots y_n]_补\)。
余数 = 余数 - 除数。若余数为负，商最低位置 0，同时余数 = 余数 + 除数；若余数为正，商最低位置 1。
将余数左移一位，空位置 0；商左移一位。
将步骤 2、3 重复进行 \((n+1)\) 次，最后一次循环商不再左移。首商为 1 时除法溢出；首商为 0 时舍去首商，得到最终的商和余数。

商的初始值为 0，余数的初始值为被除数的数值位（\(0.x_1x_2\cdots x_n\)）。加除数时为 \(0.y_1y_2\cdots y_n\)，而减除数用加除数相反数的补码作为替换，为 \([0.y_1y_2\cdots y_n]_补\)。
余数 = 余数 - 除数。若余数小于 0，商最低位置 0；若余数大于 0，商最低位置 1。将商左移一位。
若余数为负，则余数左移一位后，余数 = 余数 + 除数；若余数为正，则余数左移一位后，余数 = 余数 - 除数。
将步骤 2、3 重复进行 \((n+1)\) 次，最后一次循环商不再左移。首商为 1 时除法溢出；首商为 0 时舍去首商，得到最终的商和余数。

加减交替法

符号位参加运算，商初始值为 0。对除数的减法改为加上除数相反数的补码。
若被除数与除数同号，余数 = 被除数 - 除数；若被除数与除数异号，余数 = 被除数 + 除数。
若余数与除数同号，商最低位置 1，余数左移一位后，余数 = 余数 - 除数；若余数与除数异号，商最低位置 0，余数左移一位后，余数 = 余数 + 除数。
商左移一位。
将步骤 3、4 重复进行 \((n+1)\) 次，最后一次余数和商不再左移，同时末位恒置 1。首商为 1 时除法溢出；首商为 0 时舍去首商，得到最终的商和余数。

溢出判断

Text Only

下溢 |                | 上溢
<-----+-------0-------+---->
负+负                   正+正

一位符号位数据位进位双符号位（模4补码）

实际参与操作的两个数符号相同，结果与原操作数符号不同，即溢出

符号位向高位进位记为 \(C_s\)，最高数值位进位记为 \(C_1\)，则如果 \(C_s\) 和 \(C_1\) 不同，即发生溢出

正数使用00，负数使用11，运算结果的两个符号位若不相同，则有溢出

01 为上溢，10为下溢

浮点数的表示和运算

浮点数的表示

Text Only

+-----+---------------+-----+---------------+
| Jf  |  J1J2....Jm   | Sf  |  S1S2....Sn   |
+-----+---------------+-----+---------------+
  阶符     阶码数值       数符      尾数数值
| <-   阶码 E     ->  | <-   尾数 M        ->|

阶码: 反映浮点数的表示范围及小数点的实际位置，是常用补码或移码表示的定点整数
尾数: 其数值部分的位数n反映浮点数的精度，是常用原码或补码表示的定点小数

规格化

规定尾数的最高数值位必须是一个有效值。

左规和右规
- 左规：尾数算术左移1位，阶码减1
- 右规：尾数算术右移1位，阶码加1（浮点数运算结果尾数出现溢出，双符号位01或10）
规格化尾数
原码补码
- 正数：0.10...0 ~ 0.11...1，尾数表示范围为 \([\dfrac{1}{2},1-2^{-n}]\)
- 负数：1.11...1 ~ 1.10...0，尾数表示范围为 \([-(1-2^{-n}),-\dfrac{1}{2}]\)
- 正数：0.10...0 ~ 0.11...1，尾数表示范围为 \([\dfrac{1}{2},1-2^{-n}]\)
- 负数：1.00...0 ~ 1.01...1，尾数表示范围为 \([-1,-(\dfrac{1}{2}+2^{-n})]\)

IEEE 754标准

移码=真值+偏置值，在IEEE754标准中，偏置值取的是 \(2^{n-1}-1\)

Text Only

+------+------------------+----------------+
| ms   |        E         |        M       |
+------+------------------+----------------+
  数符      阶码（移码）        尾数（原码）隐藏最高位1

类型	数符	阶码位数	尾数位数	总位数	偏置值
短浮点数float	1	8	23	32	127(7FH)
长浮点数double	1	11	52	64	1023(3FFH)
临时浮点数long double	1	15	112	128	16383(3FFFH)

规格化float真值：\((-1)^S\times 1.M\times 2^{E-127}\)

规格化double真值：\((-1)^S\times 1.M\times 2^{E-1023}\)

表示范围

最小绝对值: 尾数全为0，阶码真值最小-126，此时整体真值为 \((1.0)_2\times 2^{-126}\)
最大绝对值: 尾数全为1，阶码真值最大127，此时整体真值为 \((1.111...1)_2\times 2^{127}\)

特殊表示

阶码E全为0，尾数M不全为0时，表示非规格化小数
阶码E全为0，尾数M全为0时，表示真值 \(\pm 0\)
阶码E全为1，尾数M全为0时，表示无穷大 \(\pm \infty\)
阶码E全为1，尾数M不全为0时，表示非数值NaN

浮点数的加减运算

在计算机中，加减法运算用补码实现，两个浮点数如果要进行加减法运算，它们的阶或者指数必须相等

graph LR
  对阶-->尾数加减-->规格化-->舍入-->判溢出

对阶

在计算机中，采用小阶向大阶看齐的方法，实现对阶。

尾数求和

采用补码加法。

规格化

左规: 尾数左移一位，阶码减1，直到数符和第一数位不同为止（机器数表示方式是补码）。
右规: 尾数右移一位，阶码加1。

舍入

截断: 将移出的数据一律舍去。
0舍1入: 移掉的是1，则尾数末尾加1；移掉的是0，则不加。
（末位）恒置1法: 将要保留的末位数据恒置1，无论右移掉的是1还是0，末位是1还是0。

溢出判断

Text Only

|  上溢   |    负浮点数   | 下溢  |     正浮点数     |  上溢   |
+--------+--------------+------+-----------------+--------+
01,xxxx                 10,xxxx                   01,xxxxx

运算方法和运算电路

基本运算部件(算术逻辑单元ALU)

功能

算术运算：加减乘除
逻辑运算：与或非
辅助功能：移位、求补

ALU的结构（抽象）

Text Only

输入1       输入2
  |          |
  ↓          ↓
+----+     +----+
|    |     |    |
+    +-----+    +
|               | <--- 控制信号
+---------------+
       ↓
      输出

输入信号（操作数）
控制信号（指令译码产生）
输出信号（运算结果）

ALU的结构（实例）

Text Only

       F3-F0
         ↑
+--------------------+
|                    |
|        74181       |<- S0-S3, M
|        4位ALU      |
+--------------------+
   ↑      ↑      ↑
  B3-B0  A3-A0  C-1

S0-S3和M：来自CU控制单元的控制信号。CU分析指令的操作是什么（加减乘除/逻辑运算），CU根据其分析结果发出控制信号
- M表示的是该操作是逻辑运算还是算术运算：M = 1为逻辑运算，M = 0为算术运算
- S0 - S3表示的是将要进行哪一种逻辑运算或者算术运算：有4个bit，可以表示16种不同的运算
A0 - A3 和 B0 - B3：表示两个4bit的数据，分别从A0 - A3和B0 - B3输入
F0 - F3：经过ALU运算后，得到4bit的数据，通过F0 - F3输出

一位全加器

\[ \begin{align*} C_i&=A_iB_i+(A_i\oplus B_i)C_{i-1}\\ S_i&=A_i\oplus B_i\oplus C_{i-1} \end{align*} \]

\(C_{i-1}\)：低位的进位
\(S_i\)：本位和

Text Only

          Si
           ↑
     +------------+
Ci <-|            |<-Ci-1
     |    FA      |
     |            |
     +------------+
          ↑  ↑
         Ai  Bi

串行加法器

每次的产生的进位保存到进位触发器中，作为下次加法的进位

操作数n位，则进行n次加法

并行加法器

将n个全加器串联起来，第 \(i\) 个全加器输出的进位会作为第 \(i + 1\) 个全加器的进位输入

串行进位并行加法器并行进位并行加法器

Text Only

       Sn               S2          S1
       ↑                ↑           ↑
    +-----+           +-----+    +------+
 Cn←| FA  |←Cn-1...C2←| FA  |←C1-|  FA  |←C0
    +-----+           +-----+    +------+
     ↑  ↑               ↑ ↑        ↑  ↑
     An Bn              A2 B2      A1 B1

只与 \(C_0\) 有关

\[ \begin{align*} C_i=G_i+P_iC_{i-1}(G_i=A_iB_i, P_i=A_i\oplus B_i) \end{align*} \]

标志位生成

OFSFZFCF

溢出：最高位（n + 1位）的进位和次高位（第 n 位）的进位进行异或，对有符号数加减有意义

符号：输出结果的最高位（第n位），0正1负，对有符号数加减有意义

零：运算结果为0，则为1；结果非0，则为0

进位/借位：最高位（n + 1位）的进位和sub（1为减法，0为加法）进行异或，对无符号数加减有意义

加减运算

加法X+Y

X直接输入，Y经过多路选择器的0输入，sub的输入为0→cin为0

Text Only

       X          Y
       |          |(MUX=0)<--Sub=0
       A          B
       ↓          ↓
     +----+     +----+
Cout←|    |     |    |
     +    +-----+    +
     |               | <--- Cin=0
     +---------------+
            ↓
           输出

减法X-Y

X直接输入，Y经过多路选择器的1输入，此时，Y的数据需要经过非门（按位取反），sub的输入为1（末位+1）→cin为1

Text Only

                  Y
                  ↓(not)
       X          ~Y
       |          |(MUX=1)<--Sub=1
       A          B
       ↓          ↓
     +----+     +----+
Cout←|    |     |    |
     +    +-----+    +
     |               | <--- Cin=1
     +---------------+
            ↓
           输出

乘除运算

乘法

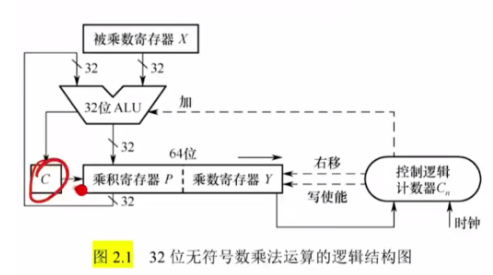
被乘数存放在被乘数寄存器X中，乘数存放在乘数寄存器Y中。

无符号数乘法补码一位乘法

乘积寄存器位P数和被乘数寄存器X、乘数寄存器Y相同，逻辑上乘积寄存器P、乘数寄存器Y和进位C是连在一起使用的（即逻辑右移时，原来的C作为现乘积寄存器的最高位，原乘积寄存器的最低位作为现乘数寄存器的最高位，原乘数寄存器的最低位舍弃）
ALU主要实现加法运算，C是两个数相加可能产生的进位：若当前乘数寄存器的最低位为0，则ALU左边输入乘积寄存器，右边输入0，计算结果输出到乘积寄存器中；若当前乘数寄存器的最低位为1，则ALU左边输入乘积寄存器，右边输入被乘数寄存器，计算结果输入到乘积寄存器中
ALU计算完成并输出数据后，进行逻辑右移
控制逻辑发出加、右移和写使能控制信号；设乘数和被乘数位n位，则计数器从n开始计数，进行n轮加法、右移，每进行一轮加法和右移后，计数器 - 1
两个n位数相乘，结果用2n位暂存，结果最终保留的是乘数寄存器中n bit，乘积寄存器舍弃。若乘积寄存器全0，则不发生溢出；只要有1，则发生溢出

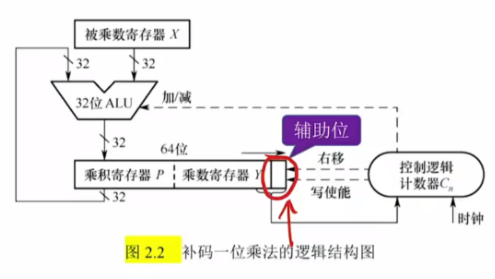
乘积寄存器位P数和被乘数寄存器X、乘数寄存器Y相同，逻辑上乘积寄存器P、乘数寄存器Y和辅助位是连在一起使用的（即算术右移时，原乘积寄存器的最低位作为现乘数寄存器的最高位，原乘数寄存器的最低位作为现辅助位，辅助位舍弃）
ALU主要实现加法运算：根据辅助位和乘数寄存器的最低位进行加/减法
- 辅助位 - 乘数寄存器最低位 = 1，乘积寄存器 + X的补码
- 辅助位 - 乘数寄存器最低位 = 0，不做加法
- 辅助位 - 乘数寄存器最低位 = -1，乘积寄存器 + （-X）的补码（逻辑减法，实际加法）
ALU计算完成并输出数据后，进行算术右移（用符号位补空位）
控制逻辑发出加、右移和写使能控制信号；设乘数和被乘数位n位，则计数器从n开始计数，进行n轮加法、右移，每进行一轮加法和右移后，计数器 - 1
两个n位数相乘，结果用2n位暂存，结果最终保留的是乘数寄存器中的n bit，乘积寄存器舍弃。若高n + 1 bit为全0或全1，则不溢出；否则，溢出

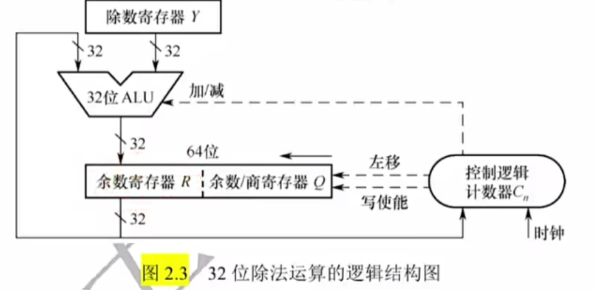
除法

n位定点数的除法运算，实际上是用一个2n位的数去除以一个n位的数，得到一个n位的商，因此需要对被除数进行扩展。

对于n位定点正小数，只要在被除数低位添n个0即可；对于n位定点正整数，只要在被除数的高位添n个0即可。