数组¶
ADT类型定义¶
- 数据对象 \(D=\{a_{j_1,j_2,..,j_i,...j_N} | j_i = 0,..., b_i -1, i=1,2,..,N a_{j_1,j_2,..,j_i,...j_N} \in ElemSet \}\)
- 称 N(>0) 为数组的维数,\(b_i\) 为数组第 i 维的长度,\(j_i\) 为数组元素的第i维下标
-
数据关系
\[ \begin{equation}\begin{split} &R=\{R_1,R_2,...,R_N\} \\ &R_i = \{\left \langle a_{j_1,j_2,..,j_i,...j_N},a_{j_1,j_2,..,j_i,...j_N}\right \rangle |0 \leq j_k \leq b_k-1, 1 \leq k \leq N \\ \text{且} &k \neq i, 0\leq j_i \leq b_i -2, a_{j_1 ,...,j_i ,...,j_N}, a_{j_1 ,...,j_i +1 ,...,j_N} \in D,i=2,...,N\} \end{split}\end{equation} \] -
基本操作
InitArray (&A, n, bound1, ..., boundn)- 操作结果:若维数 n 和各维长度合法,则构造相应的数组 A。
DestroyArray (&A)- 初始条件:数组 A 已经存在。
- 操作结果:销毁数组 A。
Value (A, &e, index1, ..., indexn)- 初始条件:A 是 n 维数组,e 为元素变量,随后是 n 个下标值。
- 操作结果:若各下标不超界,则e赋值为所指定的A的元素值,并返回OK。
Assign (&A, e, index1, ..., indexn)- 初始条件:A 是 n 维数组,e 为元素变量,随后是 n 个下标值。
- 操作结果:若下标不超界,则将 e 的值赋给A中指定下标的元素。
存储表示——顺序存储¶
- 将数组元素按行排列,第i+1个行向量紧接在第i个行向量后面
- 在PASCAL、C语言中是这样
- 将数组元素按列排列,第j+1个列向量紧接在第j个列向量之后
- FORTRAN语言即是如此
推广到多维数组
- 行优先顺序可规定为先排最右的下标,从右到左,最后排最左下标;列优先顺序与此相反,先排最左下标,从左向右,最后排最右下标
- 以二维数组为例,二维数组
R[m][n]中每个数据元素占L个存储地址,并以LOC(i, j) 表示下标为 (i, j) 的数据元素的存储地址,则该数组中任何一对下标 (i, j) 对应的数据元素- 在以行为主的顺序映象中存储地址为 \(LOC (i, j) = LOC(0,0) + (i \times n + j) \times L\)
- 在以列为主的顺序映象中存储地址为 \(LOC (i, j) = LOC(0,0) + (j \times m + i) \times L\)
矩阵的压缩存储¶
对称矩阵¶
- 在一个n阶方阵A中,若元素满足下述性质:\(a_{ij} =a_{ji},0 \le i,j \le n-1\) 则称A为对称矩阵
- 对称矩阵的元素关于主对角线对称,只需要用一个数组存放下三角或上三角的元素即可,这个一维数组的长度为 \(\frac {(1+n)n}{2}\)
- 令 \(I=max(i,j), J=min(i,j)\),则有
\[
\begin{equation}\begin{split}
&k=I \times \frac {I+1}{2}+J (0 \leq k \lt \frac {n(n+1)}{2}) \\
&LOC(a_{ij})=LOC(sa[k])=LOC(sa[0])+k \times L=LOC(sa[0])+[ I× (I+1)/2+J ] \times L
\end{split}\end{equation}
\]
三角矩阵¶
- 以主对角线划分,三角矩阵有上三角和下三角两种。上三角矩阵的下三角(不包括主对角线)中的元素均为常数。下三角矩阵正好相反,它的主对角线上方均为常数。在大多数情况下,三角矩阵常数为零。
- 三角矩阵中的重复元素c可共享一个存储空间,其余的元素正好有 \(\frac {(1+n)n}{2}\) 个,可压缩存储到向量
sa[0..n(n+1)/2]中,其中c存放在向量的最后一个分量中 -
如果A是一个上三角矩阵,sa[k]和\(a_{ij}\)的对应关系为
\[ k= \begin{cases} i(2n-i+1)/2+j-i &i \leq j \\ n(n+1)/2 &i \gt j \end{cases} \] -
如果A是一个下三角矩阵,sa[k]和\(a_{ij}\)的对应关系为
\[ k= \begin{cases} i(i+1)/2+j & i \leq j \\ n(n+1)/2 & i \gt j \end{cases} \]
对角矩阵¶
- 非零元素仅出现在主对角上(\(a_{ii},0≦i≦n-1\)) , 紧邻主对角线上面的那条对角线上(\(a_{i,i+1} ,0≦i≦n-2\))和 紧邻主对角线下面的那条对角线上(\(a_{i+1,i} ,0≦i≦n-2\))。
- 显然,当 \(\lvert i-j \rvert \gt 1\) 时,元素\(a_{ij} =0\)。
- 对角矩阵可按行优先顺序或对角线的顺序,将其压缩存储到一个向量中,并且也能找到每个非零元素和向量下标的对应关系。
- 这个向量的长度是\(3n-2\)
- 例如:一个三对角带状矩阵,除满足条件i=0,j=0、1,或i=n-1,j=n-2、n-1或1<i<n-1,j=i-1、i、i+1的元素\(a_{ij}\) 外,其余元素都是零
-
那么,它的非零元素和向量下标的对应关系为
\[ LOC(i,j)=LOC(0,0)+[3×i-1+(j-i+1)] ×L=LOC(0,0)+(2i+j) ×L \]
稀疏矩阵¶
- 假设在 m×n 的矩阵中有 t 个非零值元,令 \(\delta=\frac {t}{m\times n}\),称 \(\delta\) 为矩阵的稀疏因子,则通常认定 \(\delta \le0.05\) 的矩阵为稀疏矩阵。
-
三元组顺序表:以顺序存储结构作为三元组线性表的存储结构,由此得到的稀疏矩阵的一种压缩存储方法,称之谓三元组顺序表。例如
\[ M= \begin{bmatrix} 0 & 0 & 9 & 0 & -7 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 8 & 0 & 0 \\ 5 & 0 & 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 & 16 & 0 \\ \end{bmatrix} \]其三元组线性表为 ((1,3,9),(1,5,-7),(3,4,8),(4,1,5),(4,6,2),(5,5,16))
- 结构定义
-
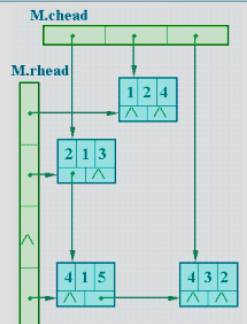
十字链表