树与二叉树

树形结构是一类重要的非线性结构。树型结构是结点之间有分支，并且具有层次关系的结构。

树的基本概念

• 树是具有n个节点的有限集合T，它满足：
  1. 有且只有一个称为“根(root)”的结点
  2. 其余的结点可分为m个互不相交的子集，每个子集又是一棵树，称其为子树(Subtree)
• T为空时，称为空树
• 树是一种层次分明的结构，约定根的层次为1，其余元素层次的定义为：若根的层次为L，子树根的层次为 L+1。
• 树的深度定义为树中叶子结点所在最大层次数。
• 如果子树之间映射客观存在次序关系，则为“有序树”，否则为“无序树”。

• 度

  结点的度树的度

  其分支的个数定义为“结点的度”，如果该值大于0，即为“分支结点”，否则为“叶子结点”。

  树中所有结点度的最大值定义为“树的度”

• 结点之间的关系

  • “根”即为树中没有前驱的结点。称根结点为子树根的“双亲”
  • 称子树根为根结点的“孩子”。“最左孩子”指的是在存储结构中存放的第一棵子树的根。
  • 根的所有子树根互为“兄弟”。“右兄弟”指存储结构中确定的有相同双亲的下一棵子树的根。
  • 结点的“祖先”指从根结点到该结点所经分支上的所有结点。
  • 以某结点为根的子树中的任一结点都称为该结点的“子孙”。
• 性质
  • 树中的结点数等于所有结点的度数+1
  • 度为m的树中第i层上至多有 \(m^{i-1}\) 个结点( \(i\ge 1\) )
  • 高度为h的m叉树至多有 \(\frac {m^h-1}{m-1}\) 个结点
  • 具有n个结点的m叉树的最小高度为 \(\lceil \log_m[n(m-1)+1] \rceil\)

ADT类型定义

• 数据对象 D是具有相同特性的数据元素的集合。
• 数据关系 若D为空集，则称为空树；若D中仅含一个数据元素，则关系R为空集；否则 R={H}：
  1. 在D中存在唯一的称为根的数据元素 root，它在关系H下无前驱；
  2. 当 \(n\gt 1\) 时，其余数据元素可分为 \(m(m\gt 0)\) 个互不相交的(非空)有限集 \(T_1,T_2, \cdots,T_m\) , 其中每一个子集本身又是一棵符合本定义的树，称为根 root 的子树，每一棵子树的根 \(x_i\) 都是根 root 的后继，即 \(\left \langle root,x_i\right \rangle \in H,i=1,2, \cdots,m\) 。

• 基本操作

  结构建立与销毁查找添加及删除数据遍历其他

  • InitTree(&T)
    • 操作结果：构造空树 T。
  • CreateTree(&T,definition)
    • 初始条件：definition 给出树T的定义。
    • 操作结果：按 definition 构造树 T。
  • DestroyTree(&T)
    • 初始条件：树 T 存在。
    • 操作结果：销毁树 T。

  • Root(T)
    • 初始条件：树 T 存在。
    • 操作结果：返回 T 的根。
  • Value(T, cur_e)
    • 初始条件：树 T 存在，cur_e 是 T 中某个结点。
    • 操作结果：返回 cur_e 的值。
  • Parent(T, cur_e)
    • 初始条件：树 T 存在，cur_e 是 T 中某个结点。
    • 操作结果：若 cur_e 是T的非根结点，则返回它的双亲，否则返回“空”。
  • LeftChild(T, cur_e)
    • 初始条件：树 T 存在，cur_e 是 T 中某个结点。
    • 操作结果：若 cur_e是T的非叶子结点，则返回它的最左孩子，否则返回“空”。
  • RightSibling(T, cur_e)
    • 初始条件：树 T 存在，cur_e 是 T 中某个结点。
    • 操作结果：若 cur_e 有右兄弟，则返回它的右兄弟，否则返回“空”。

  • Assign(T, cur_e, value)
    • 初始条件：树T存在，cur_e 是 T 中某个结点。
    • 操作结果：结点 cur_e 赋值为 value。
  • InsertChild(&T, &p, i, c)
    • 初始条件：树 T 存在，p 指向T中某个结点，1≤i≤p 所指结点的度＋1，非空树 c 与 T 不相交。
    • 操作结果：插入 c 为 T 中 p 所指结点的第 i 棵子树。
  • DeleteChild(&T, &p, i)
    • 初始条件：树 T 存在，p 指向 T 中某个结点，1≤i≤p 指结点的度。
    • 操作结果：删除 T 中 p 所指结点的第 i 棵子树。

  • TraverseTree(T, visit())
    • 初始条件：树T存在，visit 是对结点操作的应用函数。
    • 操作结果：按某种次序对 T 的每个结点调用函数visit() 一次且至多一次。一旦 visit() 失败，则操作失败。

  • ClearTree(&T)
    • 初始条件：树 T 存在。
    • 操作结果：将树 T 清为空树。
  • TreeEmpty(T)
    • 初始条件：树 T 存在。
    • 操作结果：若 T 为空树，则返回 true，否则返回 false。
  • TreeDepth(T)
    • 初始条件：树T存在。
    • 操作结果：返回T的深度。//树的深度定义为树中叶子结点所在最大层次数

二叉树

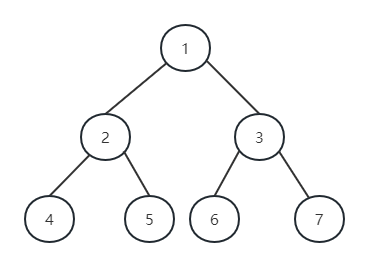
二叉树是由n(n>=0)个结点的有限集合构成，此集合或者为空集，或者由一个根结点及两棵互不相交的左、右子树组成，并且左右子树都是二叉树。

• 二叉树的特点
  • 每个结点至多只有两棵子树
  • 子树有左右之分，不可颠倒

ADT类型定义

• 数据对象 D 是具有相同特性的数据元素的集合
• 数据关系 若 D 为空集，称 BinaryTree 为空二叉树；若D为非空集合，则关系 R={H}：
  1. 在 D 中存在唯一的称为根的数据元素 root，它在关系 H 下无前驱；
  2. D 中其余元素集必可分为两个互不相交的子集 L 和 R，每一个子集都是一棵符合本定义的二叉树，并分别为 root 的左子树和右子树。如果左子树 L 不空，则必存在一个根结点 \(x_L\) ，它是 root 的“左后继”( \(\left \langle root, x_L \right \rangle \in H\) )，如果右子树 R 不空，则必存在一个根结点 \(x_R\) 为 root 的“右后继”( \(\left \langle root, x_R\right \rangle \in H\) )。

• 基本操作

  结构建立与销毁添加及删除数据查找遍历其他

  • InitBiTree(&T)
    • 操作结果：构造空二叉树 T。
  • CreateBiTree(&T, definition)
    • 初始条件：definition 给出二叉树 T 的定义。
    • 操作结果：按 definition 构造二叉树 T。
  • DestroyBiTree(&T)
    • 初始条件：二叉树 T 存在。
    • 操作结果：销毁二叉树 T。

  • Assign(&T, &e, value)
    • 初始条件：二叉树 T 存在，e 是 T 中某个结点。
    • 操作结果：结点 e 赋值为 value。
  • InsertChild(&T, p, LR, c)
    • 初始条件：二叉树 T 存在，p 指向 T 中某个结点，LR 为 0 或 1，非空二叉树 c 与 T 不相交且右子树为空。
    • 操作结果：根据 LR 为 0 或 1，插入 c 为 T 中 p 所指结点的左或右子树。p所指结点原有左或右子树成为 c 的右子树。
  • DeleteChild(&T, p, LR)
    • 初始条件：二叉树 T 存在，p 指向 T 中某个结点，LR 为 0 或 1。
    • 操作结果：根据 LR 为 0 或 1，删除 T 中 p 所指结点的左或右子树。

  • Root(T)
    • 初始条件：二叉树 T 存在。
    • 操作结果：返回 T 的根。
  • Value(T, e)
    • 初始条件：二叉树 T 存在，e 是 T 中某个结点。
    • 操作结果：返回 e 的值。
  • Parent(T, e)
    • 初始条件：二叉树 T 存在，e 是 T 中某个结点。
    • 操作结果：若e是T的非根结点，则返回它的双亲，否则返回“空”。
  • LeftChild(T, e)
    • 初始条件：二叉树 T 存在，e 是 T 中某个结点。
    • 操作结果：返回 e的左孩子。若 e 无左孩子，则返回“空”。
  • RightChild(T, e)
    • 初始条件：二叉树 T 存在，e 是 T 中某个结点。
    • 操作结果：返回 e 的右孩子。若 e 无右孩子，则返回“空”。
  • LeftSibling(T, e)
    • 初始条件：二叉树 T 存在，e 是 T 中某个结点。
    • 操作结果：返回 e 的左兄弟。若 e 是其双亲的左孩子或无左兄弟，则返回“空”。
  • RightSibling(T, e)
    • 初始条件：二叉树 T 存在，e 是 T 的结点。
    • 操作结果：返回 e 的右兄弟。若 e 是其双亲的右孩子或无右兄弟，则返回“空”。

  • PreOrderTraverse(T, visit())
    • 初始条件：二叉树 T 存在，visit 是对结点操作的应用函数。
    • 操作结果：先序遍历 T，对每个结点调用函数 visit 一次且仅一次。一旦 visit()失败，则操作失败。
  • InOrderTraverse(T, visit())
    • 初始条件：二叉树 T 存在，visit 是对结点操作的应用函数。
    • 操作结果：中序遍历 T，对每个结点调用函数 visit 一次且仅一次。一旦 visit() 失败，则操作失败。
  • PostOrderTraverse(T, visit())
    • 初始条件：二叉树T存在，visit 是对结点操作的应用函数。
    • 操作结果：后序遍历 T，对每个结点调用函数 visit 一次且仅一次。一旦 visit() 失败，则操作失败。
  • LevelOrderTraverse(T, visit())
    • 初始条件：二叉树 T 存在，visit 是对结点操作的应用函数。
    • 操作结果：层序遍历 T，对每个结点调用函数 visit 一次且仅一次。一旦 visit() 失败，则操作失败。

  • BiTreeEmpty(T)
    • 初始条件：二叉树 T 存在。
    • 操作结果：若T为空二叉树，则返回 true，否则返回 false。
  • BiTreeDepth(T)
    • 初始条件：二叉树 T 存在。
    • 操作结果：返回 T 的深度。
  • ClearBiTree(&T)
    • 初始条件：二叉树 T 存在。
    • 操作结果：将二叉树 T 清为空树。

性质

• 在二叉树的第 \(i\) 层上至多有 \(2^{i-1}\) 个结点( \(i \ge 1\) )
• 深度为 \(k\) 的二叉树至多有 \(2^k-1\) 个结点( \(k \ge 1\) )

• 对任何一棵二叉树 ，如果其终端(叶子)结点数为 \(n_0\) ，度为2 的结点数为 \(n_2\) ，则 \(n_0 = n_2 + 1\) 。

  证明

  设二叉树中度为1的结点数为 \(n_1\) ，二叉树中总结点数为\(N\)，因为二叉树中所有结点均小于或等于2，所以有：

  \[ \begin{equation} N=n_0 + n_1 + n_2 \tag{1} \end{equation} \]

  再看二叉树中的分支数，除根结点外，其余结点都有一个进入分支，设B为二叉树中的分支总数，则有：\(N=B+1\) 。由于这些分支都是由度为1和2的结点射出的，所以有：

  \[ \begin{align} B&=n_1 +2×n_2 \notag \\ N&=B+1=n_1+2×n_2+1 \tag{2} \end{align} \]

  由式（1）和（2）得到：

  \[ \begin{align} n_0 +n_1 +n_2 &=n_1 +2 \times n_2 +1 \\ n_0 &=n_2 +1 \end{align} \]

满二叉树

深度为 \(k\) ，且含有 \(2^k-1\)个结点的二叉树。

一棵有7个结点的满二叉树

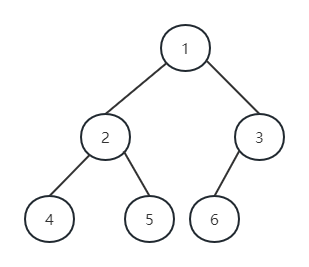
完全二叉树

如果深度为k、有n个结点的二叉树中，当且仅当其每一个结点能够与深度为k的顺序编号的满二叉树从1 到n标号的结点相对应，则称这样的二叉树为完全二叉树。

一棵有6个结点的完全二叉树

• 性质

  • 所有的叶结点只可能在层次最大的两层上出现
  • 对任一结点，如果其右子树的最大层次为L，则其左子树的最大层次为L 或 L ＋1

  • 具有n 个结点的完全二叉树的深度为 \(\lfloor log_2n \rfloor +1\)

    证明

    假设此二叉树的深度为k，则根据性质2及完全二叉树的定义得到： \(2^{k-1} -1<n≤2^k -1 或 2^{k-1} ≤n<2^k\)

    取对数得到：\(k-1≤log_2n<k\) ， 即 \(\log_2 n<k≤\log_2n + 1\)

    因为k是整数。所以有：\(k=\lfloor log_2n \rfloor +1\)

  • 如果对一棵有n个结点的完全二叉树的结点按层序编号，则对任一结点 \((1 \le i \le n)\) 有

    1. 如果i=1，则结点i无双亲，是二叉树的根；如果i>1，则其双亲PARENT(i)是结点 \(\left[ i/2 \right]\) 。
    2. 如果2i>n，则结点i为叶子结点，无左孩子；否则，其左孩子LCHILD(i)是结点2i。
    3. 如果2i＋1>n，则结点i无右孩子；否则，其右孩子RCHILD(i)是结点2i＋1。

存储结构

顺序存储

按照自上而下、自左至右的顺序，遍历完全二叉树上的结点元素， 并顺次存储在一维数组中。一般用于存储完全二叉树

C

#define MAX_TREE_SIZE 100
typedef TElemType SqBiTree[MAX_TREE_SIZE];
SqBiTree bt;

Text Only

例：
            a
            |
       ----------
       |        |
       b        c
  -----      ----
  |          |
  d          e
的存储方式为
  1 2 3 4 5 6
  a b c d 0 e

链式存储

二叉树的常用存储结构是链表

二叉链表三叉链表

C

typedef struct BiTNode {
    TElemType data;
    struct BiTNode *lchild,*rchild; // 左右孩子指针
} BiTNode,*BiTree;

C

typedef struct TriTNode {
    TElemType data;
    struct TriTNode *Lchild, *Rchild; // 左、右孩子指针
    struct TriTNode *parent; // 双亲指针
} *TriTree;

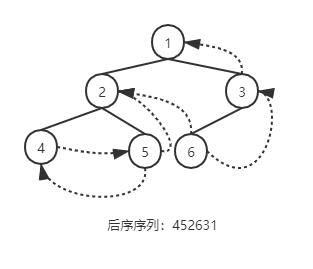
遍历二叉树

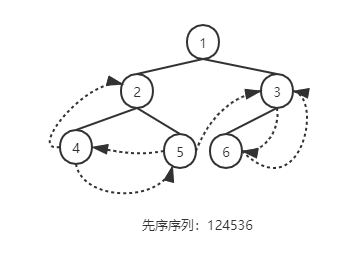
遍历二叉树的问题，就是说如何按某条搜索路径巡访树中的每一个结点，使得每一个结点均被访问一次，而且仅被访问一次。

先序遍历中序遍历后序遍历层次遍历

若二叉树为空，则空操作；否则（1）访问根结点；（2）先序遍历左子树；（3）先序遍历右子树。

C

void Preorder(BiTree T)
{
    if(T!=NULL){
        visit(T);
        Preorder(T->lchild);
        Preorder(T->rchild);
    }
}

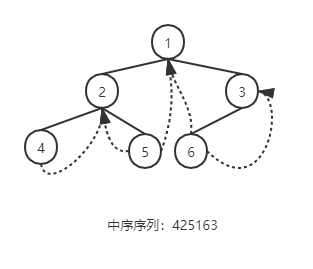
若二叉树为空，则空操作；否则（1）中序遍历左子树；（2）访问根结点；（3）中序遍历右子树。

递归算法非递归算法

C

void Inorder(BiTree T)
{
    if(T!=NULL){
        Inorder(T->lchild);
        visit(T);
        Inorder(T->rchild);
    }
}

C

void Inorder(BiTree T)
{
    InitStack(S);
    BiTree p = T;
    while(p||!IsEmpty(S)){
        if(p){
            push(S,p);
            p=p->lchild;
        }
        else{
            Pop(S,p);
            visit(p);
            p=p->rchild;
        }
    }
}

若二叉树为空，则空操作；否则（1）后序遍历左子树；（2）后序遍历右子树；（3）访问根结点。

C

void Postorder(BiTree T)
{
    if(T!=NULL){
        Postorder(T->lchild);
        Postorder(T->rchild);
        visit(T);
    }
}

从根节点开始，由上至下，从左至右，依次访问

C

void LevelOrder(BiTree T)
{
    InitQueue(Q);
    BiTree p;
    EnQueue(Q,T);
    while(!isEmpty(Q)){
        DeQueue(Q,p);
        visit(p);
        if(p->lchild!=NULL) EnQueue(Q,p->lchild);
        if(p->rchild!=NULL) EnQueue(Q,p->rchild);
    }
}

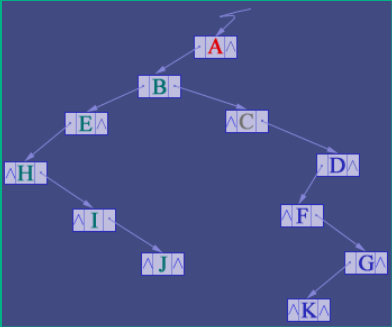
线索二叉树

先序线索树中序线索树后序线索树

当以二叉链表作为存储结构时，只能找到结点的左右孩子的信息，而不能在结点的任一序列的前驱与后继信息，这种信息只有在遍历的动态过程中才能得到，为了能保存所需的信息，可增加标志域。以这种结构构成的二叉链表作为二叉树的存储结构，叫做线索链表，其中指向结点前驱与后继的指针叫做线索。加上线索的二叉树称之为线索二叉树。

Text Only

    ----------------------------------------
    | ltag | lchild | data | rchild | rtag |
    ----------------------------------------

    其中LTag = 0表示lchild指向左孩子，LTag = 1表示lchild指向前驱；
    RTag = 0表示rchild指向右孩子，RTag = 1表示rchild指向后继。

C

typedef enum PointerType{ Link=0, Thread=1 };
// 定义指针类型，以 Link 表示指针，Thread 表示线索
typedef struct BiThrNode{
    TElemType data;
    struct BiThrNode *Lchild, *Rchild; // 左右指针
    PointerType LTag, RTag; // 左右指针类型标志
} BiThrNode, *BiThrTree;

• 线索化算法：线索化左子树→根→线索化右子树（中序）

  对 p 指向根结点的二叉树进行中序遍历，遍历过程中进行“中序线索化”。若p所指结点的左指针为空，则将它改为“左线索”，若 pre 所指结点的右指针为空，则将它改为“右线索”。指针 pre 在遍历过程中紧随其后，即始终指向 p 所指结点在中序序列中的前驱。

  void InThreading(BiThrTree p)
  {
      if (p) {
          InThreading(p->Lchild); // 对左子树进行线索化
          if (!p->Lchild) {
              p->LTag = Thread;
              p->Lchild = pre;
          } // 建前驱线索
          if (!pre->Rchild) {
              pre->RTag = Thread; pre->Rchild = p;
          } // 建后继线索
          pre = p; // 保持 pre 指向 p 的前驱
          InThreading(p->Rchild); // 对右子树进行线索化
      } // if
  } // InThreading
  

• 线索化中序遍历

  C

  void Inorder(BiThrNode *T){
      for(BiThrNode *P = Firstnode(T);p!=NULL;p=Nextnode(p)) visit(p);
  }
  
  BiThrNode *Firstnode(BiThrNode *p){
    while(p->ltag==0) p=p->lchild;
    return p;
  }
  
  BiThrNode *Nextnode(BiThrNode *p){
      if(p->rtag==0) return Firstnode(p->rchild);
      else return p->rchild;
  }
  

树与森林

• 定义森林为 m(m≥0) 棵互不相交的树的集合。则对树中每个结点而言，其子树的集合即为森林

• 从另外一个角度来说，可定义树是一个二元组 Tree = (root,F)，其中，root 是数据元素，称作树的根，F 是子树森林，记作 \(F=(T_1,T_2,\cdots ,T_m)\) ，其中 \(T_i=(r_i，F_i)\) 称作根 root 的第 i 棵子树，当 \(m≠0\) 时，在树根和其子树森林之间存在下列关系：

  \[ RF=\{\left \langle root，r_i\right \rangle | i=1,2,\cdots ,m, m\gt 0\} \]

某树的可能结构

双亲表示法孩子表示法孩子兄弟表示法

假设以一组连续空间存储树的结点，同时在每个结点中附设一个指示器指示其双亲结点在链表中的位置，其形式说明如下：

C

#define MAX_TREE_SIZE 100
typedef struct PTNode { // 结点结构
    TElemType data;
    int parent; // 双亲位置域
} PTNode;
typedef struct { // 树结构
    PTNode nodes[MAX_TREE_SIZE];
    int r, n; // 根的位置和结点数
} PTree;

上述例子可以表示为

	data	parent
0	A	-1
1	B	0
2	C	0
3	D	0
4	E	1
5	F	3
6	G	3
7	H	4
8	I	4
9	J	4
10	K	6
	r=0	n=11

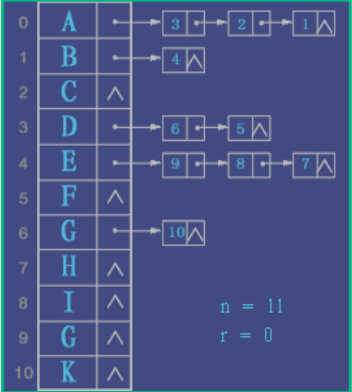
由于树中每个结点可能有多棵子树，可用多重链表来表示，即每个结点有多个指针域，其中每个指针指向一个子树的根结点。

C

孩子结点结构：
typedef struct CNode { // 孩子结点
    int child;
    struct CNode *next;
} *CNode;
双亲结点结构：
typedef struct {
    ElemType data; // 结点的数据元素
    struct CNode* firstchild; // 孩子链表头指针
} PNode;
树结构：
typedef struct {
    PNode nodes[MAX_TREE_SIZE];
    int n, r; // 结点数和根结点的位置
} CTree;

上述例子可以表示为

树中每个结点都设有两个指针，firstchild 指向该结点的“第一个”子树根结点，nextsibling 指向它的“下一个”兄弟结点。（二叉链表）

C

typedef struct CSNode{
    ElemType data;
    struct CSNode *firstchild, *nextsibling;
} CSNode, *CSTree;

上述例子可以表示为

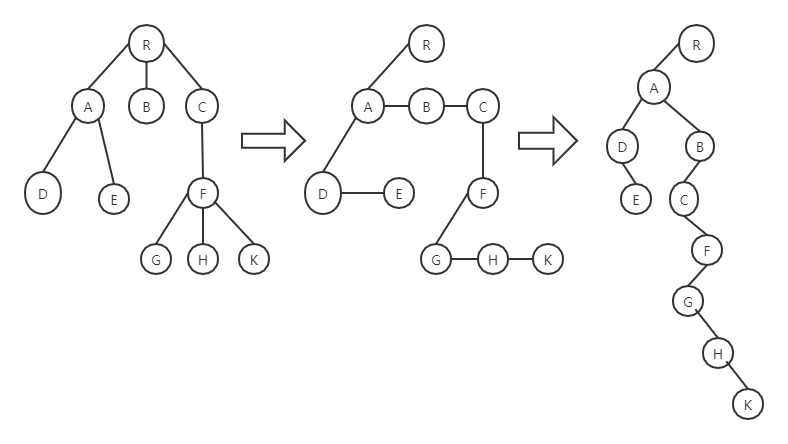
树与二叉树的转换

树→二叉树

每个结点左指针指向它的第一个孩子结点，右指针指向它在树中相邻的兄弟结点。

森林与二叉树的转换

森林→二叉树二叉树→森林

• 如果\(F = \{ T_1, T_2,\cdots , T_m \}\) 是森林，则可按如下规则转换成一棵二叉树 \(B =(root, LB, RB)\) ：
  1. 若森林 F 为空集，即 \(m=0\) ，则二叉树 B 为空树；
  2. 若森林 F 非空，即 \(m≠0\) ，则B的根root即为森林中第一棵树的根结点 \(ROOT(T_1)\) ；B的左子树LB是从 \(T_1\) 中根结点的子树森林 \(\{T_{11} , T_{12} , \cdots, T_{1m_{1}} \}\) 转换而成的二叉树；其右子树RB是从森林中删去第一棵树之后由其余树构成的森林 \(F'=\{T_2,T_3 ,\cdots , T_m \}\) 转换而成的二叉树。

• 如果 \(B =(root, LB, RB)\) 是一棵二叉树，则可按如下规则转换成森林 \(F = \{ T_1, T_2 , \cdots ,T_m \}\)：
  1. 若B为空，则F为空；
  2. 若B非空，则F中的第一棵树 \(T_1\) 的根 \(ROOT(T_1)\) 即为二叉树B的根root； \(T_1\) 中根结点的子树森林 \(F_1\) 是由左子树LB转换而成的森林；F中除 \(T_1\) 之外其余树组成的森林 \(F’=\{T_2 ,T_3 ,\cdots ,T_m \}\) 是由B的右子树RB转换而成的森林。

树和森林的遍历

先根遍历树后根遍历树先序遍历森林中序遍历森林

若树不空，则先访问根结点，然后依次从左到右先根遍历根的各棵子树。

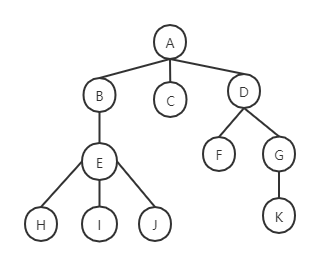
例如，对上图的先根遍历序列为ABEHIJCDFGK

若树不空，则先依次从左到右后根遍历根的各棵子树，然后访问根结点。

例如，对上图的后根遍历序列为HIJEBCFKGDA

若森林不空，则可依下列次序进行遍历：(1) 访问森林中第一棵树的根结点；(2) 先序遍历第一棵树中的子树森林；(3) 先序遍历除去第一棵树之后剩余的树构成的森林。

上述森林的先序遍历序列为ADEBCFGHK

若森林不空，则可依下列次序进行遍历：(1) 中序遍历第一棵树中的子树森林；(2) 访问森林中第一棵树的根结点；(3) 中序遍历除去第一棵树之后剩余的树构成的森林。

上述森林的中序遍历序列为DEABGHKFC

• 树的先根遍历，即森林的先序遍历可对应到二叉树的先序遍历；
• 树的后根遍历，即森林的中序遍历可对应到二叉树的中序遍历

树与二叉树的应用

并查集

并查集是一种树形的数据结构，用于处理一些不交集的合并及查询问题

初始化查操作并操作

C

void makeSet(int size) {
  for (int i = 0; i < size; i++) fa[i] = i;  // i就在它本身的集合里
  return;
}

C

int fa[MAXN];
int find(int x) {
  if (fa[x] == x)
    return x;
  else
    return find(fa[x]);
}

C

void unionSet(int x, int y) {
  x = find(x);
  y = find(y);
  if (x == y)
    return;
  fa[x] = y;
}

二叉排序树(BST)

• 性质
  • 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值。
  • 若它的右子树不空，则右子树上所有节点的值均大于其根节点的值。
  • 它的子树也是二叉排序树。

以下，定义二叉排序树结构为

C

typedef struct BST_Node {
    ElemType data;
    struct BST_Node *lchild, *rchild;
}BSTNode, *BSTPointer;

• 查找

  C++

  BSTNode* BST_Search(BiTree T,ElemType key,BSTNode *&p)
  {
      p = NULL;
      while(T!=NULL && key!=T->data){
          p = T;
          if(key<T->data) T=T->lchild;
          else T= T->rchild;
      }
      return p;
  }
  

• 插入

  • 插入新元素时，可以从根节点开始，遇键值较大者就向左，遇键值较小者就向右，一直到末端，就是插入点。

    C++

    bool BST_Insert(BiTree &T,KeyType k){
        if(T==NULL){
            T=(BiTree)malloc(sizeof(BSTNode));
            T->key = k;
            T->lchild = T->rchild = NULL;
            return true;
        }
        else if(k==T->key) return false;
        else if(k<T->key) return BST_Insert(T->lchild,k);
        else return BST_Insert(T->rchild,k);
    }
    

  • 构建一棵新的二叉排序树

    C++

    void Create_BST(BiTree &T,KeyType str[],int n){
        T=NULL;
        int i=0;
        while(i<n){
            BST_Insert(T,str[i]);
            i++;
        }
    }
    

• 删除

  • 分为三种情况

    是叶子结点有一个子结点有两个子结点

    直接删除，原BST不受影响

    将A的子节点连至A的父节点上，并将A删除

    以右子树内的最小节点取代A

平衡二叉树(AVL)

定义：它或者是一颗空树，或者具有以下性质的二叉排序树

• 它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1
• 它的左子树和右子树都是一颗平衡二叉树。

AVL树的平衡调整

统一约定AVL树的结构为

C

typedef struct Node
{
    int key;
    struct Node *left;
    struct Node *right;
    int height;
}

LL型调整RR型调整LR型调整RL型调整

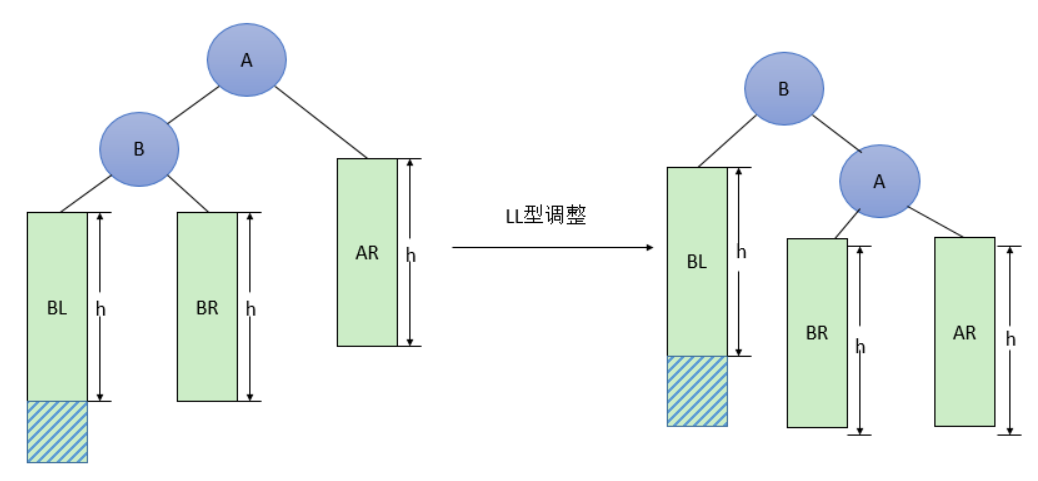
由于在A的左孩子B的左子树BL(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡(h表示子树的深度)。（双右旋）调整方法如下：

1. 将A的左孩子B提升为新的根结点
2. 将原来的根结点A降为B的右孩子
3. 各子树按大小关系连接(BL和AR不变，BR调整为A的左子树)。

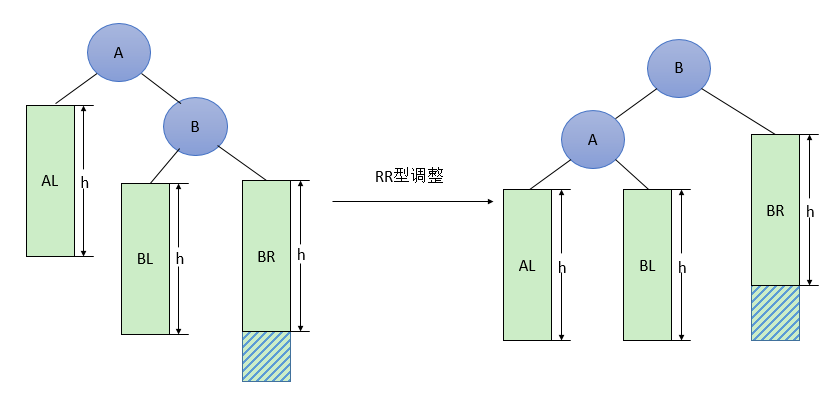
由于在A的右孩子B的右子树BR(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡(h 表示子树的深度)。（双左旋）调整方法如下：

1. 将A的右孩子B提升为新的根结点
2. 将原来的根结点A降为B的左孩子
3. 各子树按大小关系连接(AL和BR不变，BL调整为A的右子树)。

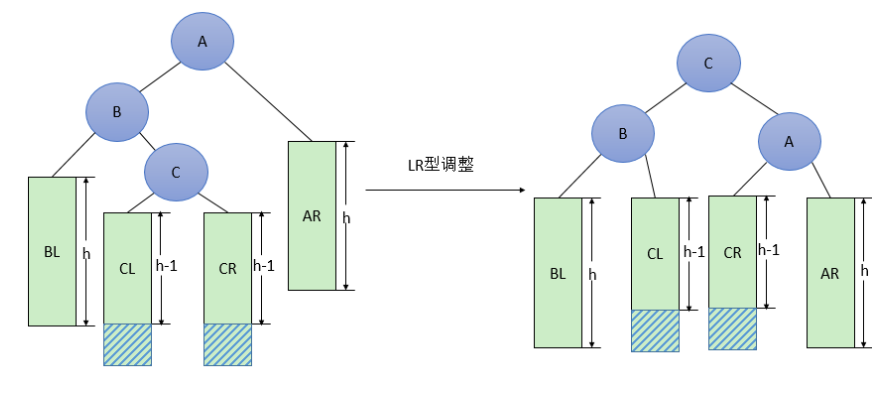
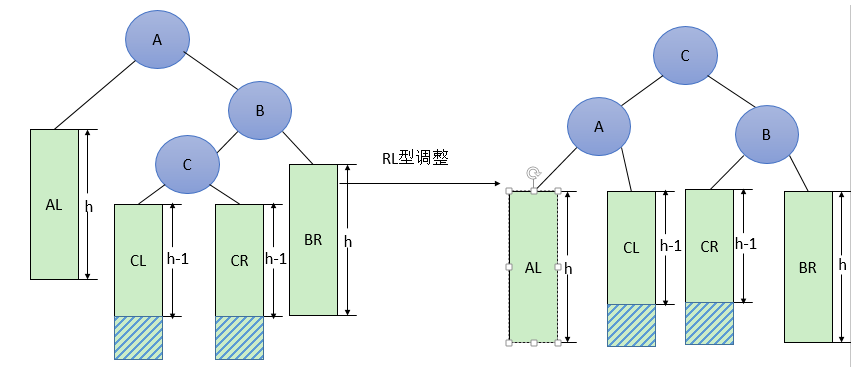
由于在A的左孩子B的右子树(根结点为C，不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡(h表示子树的深度)。（先左旋再右旋）调整方法如下：

1. 将B的左孩子C提升为新的根结点
2. 将原来的根结点A降为C的右孩子
3. 各子树按大小关系连接(BL和AR不变，CL和CR分别调整为B的右子树和A的左子树)。

由于在A的右孩子B的左子树(根结点为C，不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡(h表示子树的深度)。（先右旋再左旋）调整方法如下：

1. 将B的左孩子C提升为新的根结点
2. 将原来的根结点A降为C的左孩子
3. 各子树按大小关系连接(AL和BR不变，CL和CR分别调整为A的右子树和B的左子树)。

哈夫曼树

WPL，是树中所有叶结点的带权路径长度之和

\[ WPL = \sum_{i=0}^nW_iL_i \]

• 哈夫曼树又称最优树，是一类带权路径长度最短的树
• 构造算法（赫夫曼算法）：
  1. 根据给定的 n 个权值 \(\{w_1 ,w_2 ,\cdots ,w_n \}\)，构成 n 棵二叉树的集合 \(F=\{T_1 ,T_2 ,\cdots,T_n \}\)，其中每棵二叉树 \(T_i\) 中只有一个带权为 \(w_i\) 的根结点，其左右子树均空。
  2. 在 F 中选取两棵根结点的权值最小的树作为左右子树，构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。
  3. 在 F 中删除这两棵树，同时将新得到的二叉树加入 F 中。
  4. 重复(2)和(3)，直到 F 只含一棵树为止。这棵树便是所求的赫夫曼树
• 应用：前缀编码