跳转至

队列

定义

队列 双端队列
队列（上）/双端队列（下）
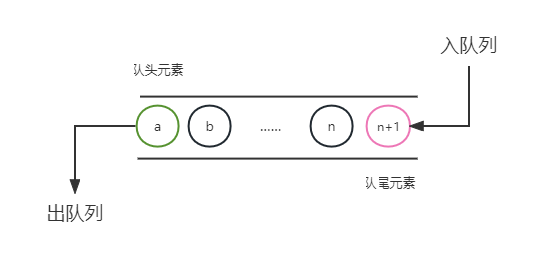
  • 队列(Queue)也是一种运算受限的线性表。它只允许在表的一端进行插入，而在另一端进行删除。允许删除的一端称为队头(front)，允许插入的一端称为队尾(rear)。
  • 因为先进入队列的成员总是先离开队列，队列亦称作先进先出(First In First Out)的线性表，简称FIFO表

ADT类型定义

  • 数据对象：\(D=\{a_i | a_i \in ElemSet, i=1,2,...,n, n≥0 \}\)
  • 数据关系：\(R1=\{\left \langle a_{i-1},a_i\right \rangle| a_{i-1},a_i \in D, i=2,...,n\}\) 约定 \(a_n\) 端为队列尾，\(a_1\) 端为队列头

  • 基本操作

    • InitQueue(&Q)
      • 操作结果：构造一个空队列 Q。
    • DestroyQueue(&Q)
      • 初始条件：队列 Q 已存在。
      • 操作结果：队列 Q 被销毁。
    • EnQueue(&Q, e)
      • 初始条件：队列 Q 已存在。
      • 操作结果：插入元素 e 为新的队尾元素
    • DeQueue(&Q, &e)
      • 初始条件：队列 Q 已存在且非空。
      • 操作结果：删除 Q 的队头元素，并用 e 返回其值。
    • GetHead(Q, &e)
      • 初始条件：队列 Q 已存在且非空。
      • 操作结果：用 e 返回Q的队头元素
    • QueueTraverse(Q,visit())
      • 初始条件：队列 Q 已存在且非空，visit() 为元素的访问函数。
      • 操作结果：依次对 Q 的每个元素调用函数 visit()。一旦 visit() 失败，则操作失败。
    • ClearQueue(&Q)
      • 初始条件：队列 Q 已存在。
      • 操作结果：将 Q 清为空队列。
    • QueueEmpty(Q)
      • 初始条件：队列Q已存在。
      • 操作结果：若 Q 为空队列，则返回 TRUE，否则返回 FALSE。
    • QueueLength(Q)
      • 初始条件：队列 Q 已存在。
      • 操作结果：返回 Q 中元素个数，即队列的长度。

存储结构

顺序队列

C
#define MAXSIZE 100
typedef struct{
    ElemType data[MAXSIZE];
    int front,rear;
}SqQueue;

循环静态顺序队列

  • 最大限度的利用数组空间
  • 出入队列时修改指针注意对maxsize取余
    • 初始化建空队列时，令 front=rear=0；
    • 每当插入一个新的队尾元素后，尾指针 rear增1；
    • 每当删除一个队头元素之后，头指针front增1。
  • 队列中一共有 \((rear+Maxsize-front) \% Maxsize\) 个元素
  • 判满：(Q.rear+1)%maxsize==Q.front
C
#define MAXQSIZE 50
typedef struct
{
    ElemType *base;    /* 初始化的动态分配存储空间 */
    int front;       /* 头指针，若队列不空，指向队列头元素 */
    int rear;        /* 尾指针，若队列不空，指向队列尾元素的下一个位置 */
}SqQueue;

  • 基本操作的实现(循环的顺序队列)

    C
    Status InitQueue(SqQueue &Q)
{
// 构造一个最大存储空间为 maxsize 的空队列 Q
    Q.base = (ElemType*)malloc(MAXQSIZE * sizeof(ElemType));
    // 为循环队列分配存储空间
    if (!Q.base) exit(OVERFLOW); // 存储分配失败
    Q.front = Q.rear = 0;
    return OK;
} // InitQueue
    C++
    bool isEmpty(SqQueue Q)
{
    return Q.rear==Q.front;
}
    C
    Status EnQueue(SqQueue &Q, ElemType e)
{
    // 若当前队列不满，就在当前队列的尾元素之后，插入元素 e 为新的队列尾元素
    if ((Q.rear + 1) % MAXQSIZE == Q.front ) //注意判满的方法
    return ERROR;
    Q.base[Q.rear] = e;
    Q.rear = (Q.rear+1) % MAXQSIZE;
    return OK;
}
    C++
    bool EnQueue(SqQueue &Q,ElemType e)
{
    if(Q.rear+1>=MAXSIZE) return false;
    else{
        Q.data[Q.rear] = e;
        Q.rear = Q.rear + 1;
        return true;
    }
}
    C
    Status DeQueue (SqQueue &Q, ElemType &e)
{
    // 若队列不空，则删除当前队列Q中的头元素，用 e 返回其值
    if (Q.front == Q.rear) //注意判空的方法
    return ERROR;
    e = Q.base[Q.front];
    Q.front = (Q.front+1) % MAXQSIZE;
    return OK;
}
    C++
    bool DeQueue(SqQueue &Q,ElemType &e)
{
    if(Q.rear==Q.front) return false;
    else{
        e = Q.data[Q.front];
        Q.front = Q.front +1;
        return true;
    }
}

链队列

  • 队列的链式存储结构简称为链队列，它是限制仅在表头删除和表尾插入的单链表。

  • 结构定义

    C
    typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
}LinkNode,*LinkQueuePtr;
typedef struct{
    LinkNode *front, *rear;
}LinkQueue;

  • 基本操作的实现

    构造一个空队列 Q

    C
    Status InitQueue (LinkQueue &Q)
{
    Q.front = Q.rear = (LinkQueuePtr)malloc(sizeof(LinkNode));
    if (!Q.front) exit(OVERFLOW); // 存储分配失败
    Q.front->next = NULL;
    return OK;
}

    销毁队列 Q

    C
    Status DestroyQueue(LinkQueue &Q)
{
    while(Q.front)
    {
        Q.rear = Q.front->next;
        free(Q.front);
        Q.front = Q.rear;
    }
    free(Q);
    Q = NULL;
    return OK;
}

    在当前队列的尾元素之后，插入元素 e 为新的队列尾元素

    C
    Status EnQueue(LinkQueue &Q,ElemType e)
{
    p = (LinkQueuePtr) malloc(sizeof(LinkNode));
    if (!p) exit(OVERFLOW); // 存储分配失败
    p->data=e; p->next = NULL;
    Q.rear->next = p; // 修改尾结点的指针
    Q.rear = p; // 移动队尾指针
    return OK;
}

    若队列不空 ，则删除当前队列 Q 中的头元素,用 e 返回其值 ，并返回 TRUE，否则返回 FALSE

    C
    Status DeQueue(LinkQueue &Q, ElemType &e)
{
    if (Q.front == Q.rear) // 链队列中只有一个头结点
    return FALSE;
    p = Q.front->next;
    e = p->data; // 返回被删元素
    Q.front->next = p->next; // 修改头结点指针
    if(Q.rear == p) Q.rear = Q.front;
    free(p); // 释放被删结点
    return OK;
}

应用

树的层次遍历

核心思想

每次出队一个元素，就将该元素的孩子节点加入队列中，直到队列中元素个数为0时，出队的顺序就是该二叉树的层次遍历结果。

c++代码写法
vector<vector<int>> levelOrder(TreeNode *root) {
    if (root == nullptr) return {};
    vector<vector<int>> ans;
    queue<TreeNode *> q;
    q.push(root);
    while (!q.empty()) {
        vector<int> vals;
        for (int n = q.size(); n--;) {
            // 取出队首元素
            auto node = q.front();
            q.pop();
            // 加入至结果集
            vals.push_back(node->val);
            // 推入非空左孩子
            if (node->left)  q.push(node->left);
            // 推入非空右孩子
            if (node->right) q.push(node->right);
        }
        ans.emplace_back(vals);
    }
    return ans;
}

图的广度优先遍历

具体算法见图 > 图的广度优先遍历章节。使用了队列+辅助标记数组的方法。

评论