跳转至

排序

排序算法总结

算法 稳定性 空间复杂度 时间复杂度 顺序存储 链式存储
直接插入排序 √ √ √
折半插入排序 √ √
希尔排序 和所取增量序列相关* √
冒泡排序 √ √ √
快速排序 √ √
直接选择排序 √ √
堆排序 √ √
2-路归并排序 √ √ √
基数排序 √ -- --

** 大部分时候，可以达到 \(O(n^{1.3})\) 复杂度

本章待排序的数据结构定义如下：

C
#define MAXSIZE 20 // 一个用作示例的小顺序表的最大长度
typedef int KeyType; // 定义关键字类型为整数类型
typedef struct {
    KeyType key; // 关键字项
    InfoType otherinfo; // 其它数据项
} RecType; // 记录类型并设定关键字为整型
typedef struct {
    RecType r[MAXSIZE+1]; // r[0]闲置或作为判别标志的“哨兵”单元
    int length; // 顺序表长度
} SqList； // 顺序表类型

概念

排序(Sorting)是计算机程序设计中的一种重要操作，它的功能是将一个数据元素(或记录)的任意序列，重新排列成一个按关键字有序递增或递减的序列。

  • 内部排序：排序期间元素均在内存中
  • 外部排序：排序期间元素不断在内、外存之间移动
  • 稳定性：假设 \(K_i=K_j(1 \le i \le n, 1 \le j \le n, i \neq j)\) ，且排序前后 \(R_i\)，\(R_j\) 相对顺序不变，则算法是稳定的，否则称排序算法不是稳定的

插入排序

直接插入排序

将一个记录插入到已排好序的有序表中，从而得到一个新的、记录数增1的有序表。

Text Only
    __________________________________________
    | 有序序列L[1...i-1]|  |无序序列L[i+1...n] |
    ------------------------------------------
                         ↑
                         |
    L[i]------------------

  • 算法描述：

    • 在 R[1..i-1] 中查找 R[i] 的插入位置，即确定j(0≤j<i)使得R[1..j].key≤R[i].key<R[j+1..i-1].key
    • 将 R[j+1..i-1] 中的记录后移一个位置
    • 将 R[i] 插入到 j+1 的位置
    C++
    void InsertSort(ElemType A[],int n)
{
    int i,j;
    for(i=2;i<=n;i++){
        A[0] = A[i]; // A[0]为“监视哨”
        for(j = i-1;A[0].key<A[j].key;j--) A[j+1]=A[j];
        A[j+1]=A[0];
    }
}

折半插入排序

由于插入排序的基本思想是在一个有序序列中插入一个新的记录，则可以利用“折半查找”查询插入位置，由此得到的插入排序算法为“折半插入排序”。

C++
void BInsertSort(ElemType A[],int n)
{
    int i,j;
    int low,mid,high;
    for(i=2;i<=n;i++){
        A[0]=A[i];
        low = 1;
        high = i-1;
        while(low<=high){
            mid = (low+high)/2;
            if(A[mid].key>A[0].key) high = mid -1;
            else low = mid+1;
        }
        for(j = i-1;j>=high+1;j--){
            A[j+1]=A[j];
        }
        A[high+1]=A[0];
    }
}

希尔排序(缩小增量排序)

先对待排序列进行“宏观调整”，待序列中的记录“基本有序(在序列中的各个关键字之前，只存在少量关键字比它大的记录)”时再进行直接插入排序

C++
void ShellInsert(ElemType A[],int dk){
    for(i=dk+1;i<=A.length;i++){
        if(A[i].key<A[i-dk].key){
            A[0]=A[i];
            for(j=i-dk;h<-&&A[0].key<A[j].key;j-=dk) A[j+dk]=A[j];
            A[j+dk]=A[0];
        }
    }
}

void ShellSort(ElemType A[], int dlta[], int n){
    for (int k=0; k<t; ++t) ShellInsert(L, dlta[k]); //一趟增量为 dlta[k] 的插入排序
}

交换排序

冒泡排序

依次比较相邻两个记录的关键字，若和所期望的相反，则交换这两个记录

C++
void BubbleSort(ElemType A[],int n){
    for(int i=0;i<n-1;i++){
        bool flag = false;
        for (int j=n-1;j>i;j--)
            if(A[j-1].key>A[j].key){
                swap(A[j-1],A[j]);
                flag = true;
            }
        if(!flag) return;
    }
}

快速排序

通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序 ，以达到整个序列有序。

  • 选定一个关键字介于“中间”的记录，从而使剩余记录可以分成两个子序列分别继续排序，通常称该记录为“枢轴(pivot)”

    • 在枢轴之前（后）的记录的关键字均不大（小）于它的关键字

  • 一趟快排也称“一次划分”，即将待排序列 R[s..t]“划分”为两个子序列R[s..i-1] 和 R[i+1..t]，i 为一次划分之后的枢轴位置

    C
    int Partition(ElemType A[],int low,int high)
{
    ElemType pivot = A[low];
    while(low<high){
        while(low<high && A[high]>=pivot) high--;
        A[low]=A[high];
        while(low<high && A[low]<=pivot) low++;
        A[high]=A[low];
    }
    A[low]=pivot;
    return low;
}

void QuickSort(ElemType A[],int low,int high)
{
    if(low<high){
        int pivotpos = Partition(A,low,high);
        QuickSort(A,low,pivotpos-1);
        QuickSort(A,pivotpos+1,high);
    }
}

选择排序

每一趟从后面n-i+1个元素中选取一个关键字最小（大）的元素，作为有序序列的第i个元素。

直接选择排序

在后 n-i+1 个记录中选出关键字最小的记录，并将它和第 i 个记录进行互换。

C
void SelectSort(ElemType A[],int n)
{
    for(int i=0;i<n-1;i++){
        int min = i;
        for(int j = i+1;j<n;j++)
            if(A[j]<A[min]) min = j;
        if(min != i) swap(A[i],A[min]);
    }
}

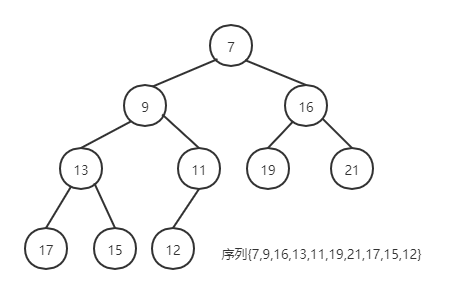
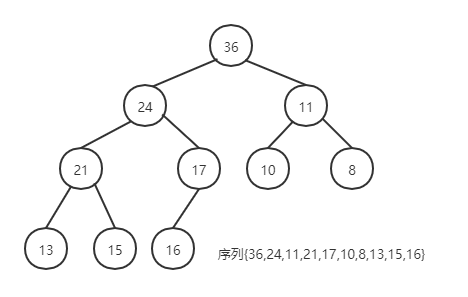
堆排序

若含n个元素的序列 \(\{k_1 ,k_2 ,\cdots ,k_n \}\) 满足下列关系则称作“小顶堆” 或“大顶堆” 。“堆顶” 元素为序列中的“最小值”或“最大值”。利用堆的特性进行的排序方法即为“堆排序”。

\[ \begin{align} \begin{cases} k_i \le k_{2i} \\ k_i \le k_{2i+1} \end{cases} 或 \begin{cases} k_i \ge k_{2i} \\ k_i \ge k_{2i+1} \end{cases} 其中，i=1,2,\cdots ,\lceil \frac {n}{2} \rceil \end{align} \]

例子

small-heap

big-heap

  • 堆的调整

    • 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换

  • 堆的初始化 从最后一个非叶子结点开始，从左至右，从下至上进行调整

  • 算法

C++
void BuildMaxHeap(ElemType A[],int len)
{
    for(int i=len/2;i>0;i--) AdjustDown(A,i,len)
}

void AdjustDown(ElemType A[],int k,int len)
{
    A[0]=A[k];
    for(int i = 2*k;i<=len;i*=2){
        if(i<len && A[i]<A[i+1]) i++;
        if(A[0]>=A[i]) break;
        else{
            A[k]=A[i];
            k=i;
        }
    }
    A[k]=A[0];
}

void HeapSort(ElemType A[],int len)
{
    BuildMaxHeap(A,len);
    for(int i=len;i>1;i--){
        swap(A[i],A[j]);
        AdjustDown(A,1,i-1);
    }
}

归并排序

将两个或两个以上的记录有序序列归并为一个有序序列。

  • 只含一个记录的序列显然是个有序序列，经过“逐趟归并”使整个序列中的有序子序列的长度逐趟增大，直至整个记录序列为有序序列止

2-路归并排序

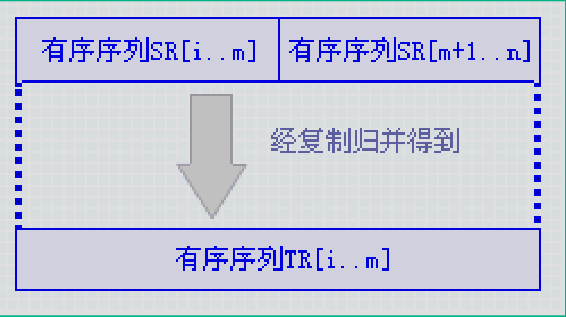
将两个相邻的有序子序列“归并”为一个有序序列。

merge-sort-2

C
void Merge(ElemType A[],int low,int mid,int high)
{
    ElemType *B = (ElemType*) malloc((n+1)*sizeof(ElemType));
    for(int k=low;k<=high;k++) B[k]=A[k];
    for(int i=low,j=mid+1,k=i;i<=mid&&j<=high;k++){
        if(B[i]<=B[j]) A[k]=B[i++];
        else A[k]=B[j++];
    }
    while(i<=mid) A[k++]=B[i++];
    while(j<=high) A[k++]=B[j++];
}

void MergeSort(ElemType A[],int low,int high)
{
    if(low<high){
        int mid = (low+high)/2;
        MergeSort(A,low,mid);
        MergeSort(A,mid+1,high);
        Merge(A,low,mid,high);
    }
}

基数排序

借助“多关键字排序”的思想，实现“单关键字排序”的算法。

  • 假设含有 n 个记录的序列为：\(\{R_1,R_2, \cdots ,R_n \}\) ，每个记录 \(R_i\) 中含有d个关键字 ，则称该记录序列对关键字有序是指：对于序列中任意两个记录 \(R_i\) 和 \(R_j\) \((1≤i<j≤n）\) 都满足下列有序关系，其中 \(K_0\) 被称作最主位关键字，\(K_{d-1}\) 被称作最次位关键字。
\[ (K_i^0,K_i^1, \cdots ,k_i^{d-1}) \lt (K_j^0,K_j^1, \cdots ,k_j^{d-1}) \]
  • 两种策略：一是最高位优先(MSD)，另一是最低位优先(LSD)
    • 最高位优先是先对 \(K^0\) 进行排序
    • 最低位优先从 \(K^{d-1}\) 先进行排序
  • 基数排序是借助 “分配”和 “收集”两种操作对单逻辑关键字进行排序的一种内部排序方法
    • 分配：按当前“关键字位”取值，将记录分配到不同的链队列中，每个队列中记录的 “关键字位” 相同
    • 收集：按当前关键字位取值从小到大将各队列首尾相链成一个链表

内部排序算法比较

  • n较小时，选择直接插入、简单排序；n较大，选择快速排序、堆排序、归并排序；n很大，且关键字位数少且可以分解，选择基数排序
  • 对于基本有序的序列，选择插入或冒泡排序
  • 记录的元素较大，可选择链式存储

外部排序

当待排序的文件比内存的可使用容量还大时，文件无法一次性放到内存中进行排序，需要借助于外部存储器（例如硬盘、U盘、光盘），这时就需要用到外部排序算法来解决。

  • 一般过程
    1. 按照内存大小，将大文件分成若干长度为 l 的子文件（l 应小于内存的可使用容量），然后将各个子文件依次读入内存，使用适当的内部排序算法对其进行排序（排好序的子文件统称为“归并段”或者“顺段”），将排好序的归并段重新写入外存，为下一个子文件排序腾出内存空间；
    2. 对得到的顺段进行合并，直至得到整个有序的文件为止。
  • 总时间=内部排序所需时间+外存信息读写时间+内部归并所需时间
  • 一般情况下对于具有 m 个初始归并段进行 k-路平衡归并时，归并的次数为：\(s=\lfloor \log_k⁡m \rfloor\)（其中 s 表示归并次数）

  • 减少归并次数，提高效率：

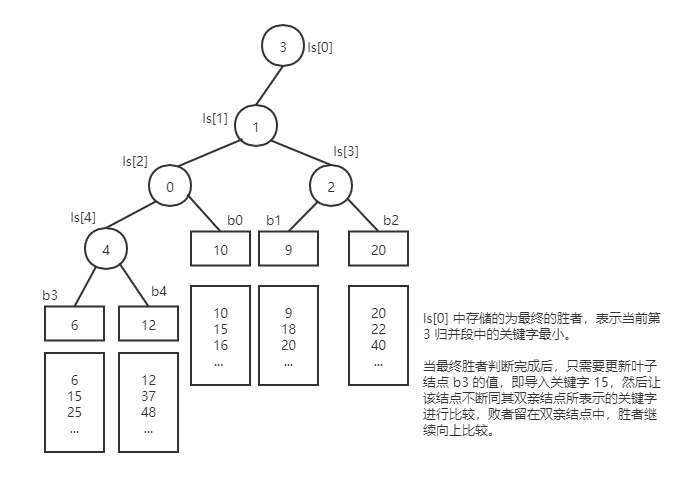
    1. 多路平衡归并算法（增加k值）

      • 失败树

        • 其双亲结点存储的是左右孩子比较之后的失败者，而胜利者则继续同其它的胜者去比较

        fail-tree

        fail-tree

    2. 置换-选择排序（减少m值,n为缓冲区容量）

      1. 首先从初始文件中输入 n 个记录到内存工作区中；
      2. 从内存工作区中选出关键字最小的记录，将其记为 MINIMAX 记录；
      3. 然后将 MINIMAX 记录输出到归并段文件中；
      4. 此时内存工作区中还剩余 n-1 个记录，若初始文件不为空，则从初始文件中输入下一个记录到内存工作区中；
      5. 从内存工作区中的所有比 MINIMAX 值大的记录中选出值最小的关键字的记录，作为新的 MINIMAX 记录；
      6. 重复过程 3—5，直至在内存工作区中选不出新的 MINIMAX 记录为止，由此就得到了一个初始归并段；
      7. 重复 2—6，直至内存工作为空，由此就可以得到全部的初始归并段。

    3. 最佳归并树

      • 仅有度为0或m的结点

      • 带权路径长度之和为归并过程中的总读记录数，总IO次数为 \(2 \times WPL\)

        merge-tree

        • 其对外存的读写次数为
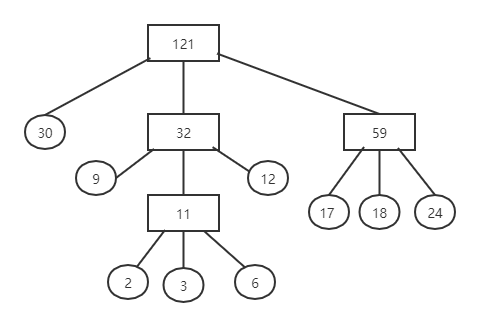
        \[ (2\times 3+3 \times 3+6 \times 3+9\times 2+12\times 2+17\times 2+18\times 2+24\times 2+30)\times 2=446 \]

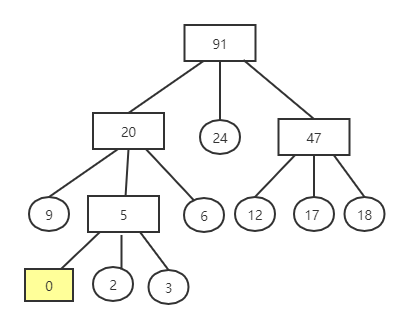
      • 通过以构建赫夫曼树的方式构建归并树，使其对读写外存的次数降至最低

        • 每次选取最小的若干个权值组成结点，叶子结点不够时，补充权值为0的结点
        • 若 \((n_0-1) \% (m-1) = 0\) ，则说明这 \(n_0\) 个叶结点可以构造 \(m\) 叉归并树，否则，有 \((n_0-1) \% (m-1) = u \neq 0\) 个叶结点多余，需要补 \(m-u-1\) 个结点

        merge-tree-2

评论