线性表

定义

由 \(n(n≧0)\) 个数据元素(结点) \(a_1,a_2,...,a_n\) 组成的有限序列，记作

\[ (a_1,a_2,..a_n) \]

• 数据元素个数n是表的长度
• \(n=0\) 时称为空表
• \(a\) 的下标 \(i\) 称为 \(a_i\) 在线性表中的位序

性质

• 在非空的线性表， 有且仅有一个开始结点 \(a_1\) ，它没有直接前趋，而仅有一个直接后继 \(a_2\)
• 有且仅有一个终端结点 \(a_n\) ，它没有直接后继，而仅有一个直接前趋 \(a_{n-1}\)
• 其余的内部结点 \(a_i(2 \leq i \leq n-1)\) 都有且仅有一个直接前趋 \(a_{i-1}\) 和一个直接后继 \(a_{i+1}\)

ADT类型定义

• 数据对象 \(D=\{a_i|a_i \in ElemSet, i=1,2,...,n, n \ge 0 \}\)
• 数据关系 \(R1=\{\left \langle a_{i-1},a_i\right \rangle|a_{i-1},a_i \in D, i=2,...,n \}\)

• 基本操作

  结构建立与销毁添加及删除数据查找遍历其他

  • InitList(&L)
    • 操作结果：构造一个空的线性表 L 。
  • DestroyList(&L)
    • 初始条件：线性表 L 已存在。
    • 操作结果：销毁线性表 L 。

  • ListInsert(&L,i,e)
    • 初始条件：线性表 L 已存在，1≤i≤LengthList(L)+1。
    • 操作结果：在 L 的第 i 个元素之前插入新的元素 e，L 的长度增1。
  • ListDelete(&L,i,&e)
    • 初始条件：线性表 L 已存在且非空，1≤i≤LengthList(L)。
    • 操作结果：删除 L 的第 i 个元素，并用 e 返回其值，L 的长度减1。
  • PutElem(&L, i, &e)
    • 初始条件：线性表 L 已存在，1≤i≤LengthList(L)。
    • 操作结果：L 中第 i 个元素赋值同 e 的值。

  • GetElem(L, i, &e)
    • 初始条件：线性表 L 已存在，1≤i≤LengthList(L)。
    • 操作结果：用 e 返回 L 中第 i 个元素的值。
  • LocateElem(L, e, compare())
    • 初始条件：线性表 L 已存在，compare() 是元素比较函数。
    • 操作结果：返回 L 中第1个与 e 满足关系 compare() 的元素的位序。若这样的元素不存在，则返回值为0。
  • PriorElem(L，cur_e，&pre_e)
    • 初始条件：线性表 L 已存在。
    • 操作结果：若cur_e是L中的数据元素，则用pre_e返回它的前驱，否则操作失败，pre_e 无定义。
  • NextElem(L, cur_e, &next_e)
    • 初始条件：线性表 L 已存在。
    • 操作结果：若cur_e是L中的数据元素，则用next_e返回它的后继，否则操作失败，next_e 无定义

  • ListTraverse(L,visit())
    • 初始条件：线性表 L 已存在，visit() 为元素的访问函数。
    • 操作结果：依次对 L 的每个元素调用函数 visit()。一旦 `visit()`` 失败，则操作失败。

  • ClearList(&L)
    • 初始条件：线性表 L 已存在。
    • 操作结果：将 L 重置为空表。
  • ListEmpty(L)
    • 初始条件：线性表L已存在。
    • 操作结果：若 L 为空表，则返回 TRUE，否则返回 FALSE。
  • ListLength(L)
    • 初始条件：线性表 L 已存在。
    • 操作结果：返回 L 中元素个数。

存储结构

顺序表

连续存储的顺序表

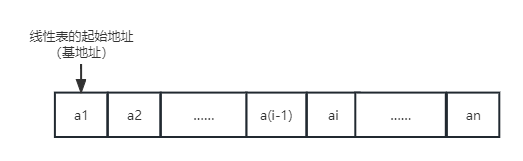
• 用一组地址连续的存储单元，依次存放线性表中的数据元素
• 以"存储位置相邻"表示位序相继的两个数据元素之间的前驱和后继的关系
• 表中第一个元素的存储位置作为线性表的起始地址，称作线性表的基地址

数据元素的存储位置

假设每个数据元素占据的存储量是一个常量 C，则后继元素的存储地址和其前驱元素相隔一个常量，即：\(LOC(a_i) = LOC(a_{i-1}) + C\) ，由此，每个数据元素的存储位置均可由第一个元素的基地址来表示，即

\[ LOC(a_i) = LOC(a_1) + (i-1) \times C \]

• 分配方式

  静态分配动态分配

  C

  #define MAXSIZE 50;
  typedef struct{
      ElemType data[MAXSIZE]; // 存储空间
      int length; // 当前长度
  }SqList_static;
  

  • 当前数组空间不够时，无法增加容量

  C

  #define MAXSIZE 50;
  typedef struct{
      ElemType *data; //存储空间基址
      int listSize; // 当前允许的最大存储容量
      int length;  // 当前长度
  }SqList_dynamic;
  

  • 基地址(data指针)使用malloc()(C)或new(C++)函数来申请，如果空间不够，可以使用realloc()(C)重新分配
  • 通常使用这种动态分配结构作为顺序表表示

• 基本操作的实现

  初始化元素定位插入元素删除元素销毁结构

  动态分配的顺序存储静态分配的顺序存储

  • 时间复杂度为 \(O(1)\)

  C++

  void InitList(SqList &L， int maxsize)
  { // 构造一个空的线性表 L
      if (maxsize == 0)  maxsize = MAXSIZE;
      L.elem = new ElemType[maxsize];
      if (!L.elem) exit(1); // 存储分配失败
      L.length = 0; // 顺序表的初始长度为0
      L.listSize = maxsize; // 该顺序表可以存储元素的最大容量
  } // InitList
  

  C++

  void initList(SqList &L)
  {
       L.length=0;
  }
  

  动态分配的顺序存储

  • 时间复杂度为 \(O(Length(L))\)

  C++

  int LocateElem(SqList L, ElemType e，void(*compare)(ElemType， ElemType))
  {
      // 在顺序表L中查找第1个值与 e 满足判定条件compare()的元素，
      // 若找到，则返回其在 L 中的位序，否则返回0。
      i = 1; // i 的初值为第1元素的位序
      p = L.elem; // p 的初值为第1元素的存储位置
      while (i <= L.length && !(*compare)(*p++ ，e))
      ++i; // 依次进行判定
      if (i <= L.length) return i;// 找到满足判定条件的数据元素为第 i 个元素
      else return 0; // 该线性表中不存在满足判定的数据元素
  } // LocateElem
  

  动态分配的顺序存储

  • 时间复杂度为 \(O(Length(L))\)

  C++

  bool ListInsert(SqList &L，int pos， ElemType e)
  {
      // 若存储空间不满且1≤pos≤Listlength(L)+1，则在顺序表 L 的第 pos 个元素前插入新元素 e 且返回TRUE，否则返回FALSE
      if (pos < 1 || pos > L.length+1) return FALSE;// 位置不合法
      if (L.length >= L.listsize) return FALSE;//存储空间已满，无法插入
      for (j=L.length-1;j>=pos-1;--j)
      L.elem[j+1] = L.elem[j];// 插入位置及之后的元素右移
      *L.elem[pos-1] = e; // 插入 e
      ++L.length; // 表长增1
      return TRUE;
  } // ListInsert
  

  动态分配的顺序存储

  • 时间复杂度为 \(O(Length(L))\)

  C++

  bool ListDelete(SqList &L， int pos， ElemType &e)
  {
      // 若1≤pos≤Listlength(L)，则以 e 带回从顺序表 L 中删除的
      // 第 pos 个元素且返回 TRUE，否则返回 FALSE
      if ((pos < 1) || (pos > L.length)) return FALSE; // 删除位置不合法
      e = *L.elem[pos-1];
      for (j = pos; j <L.length；++j)
      L.elem[j-1] = L.elem[j]; // 被删除元素之后的元素左移
      --L.length; // 表长减1
      return TRUE;
  } // ListDelete
  

  动态分配的顺序存储

  • 时间复杂度为 \(O(1)\)

  C++

  void DestroyList(SqList &L)
  {
      // 释放顺序表 L 所占存储空间
      delete[] L.elem;
      L.listsize = 0;
      L.length = 0;
  } // DestroyList_Sq
  

链表

单链表

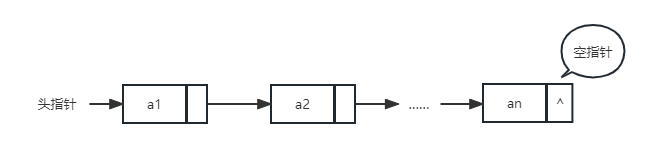
• 用一组任意的存储单元存储线性表的数据元素
• 对数据元素 \(a_i\) 来说，除了存储其本身的信息之外，还需存储一个指示其直接后继的信息（指针）
• 以第一个数据元素的存储地址作为线性表的基地址，通常称它为头指针，线性表中所有数据元素都可以从头指针出发找到
• 单链表的最后一个元素的指针域是特殊的的，用NULL表示
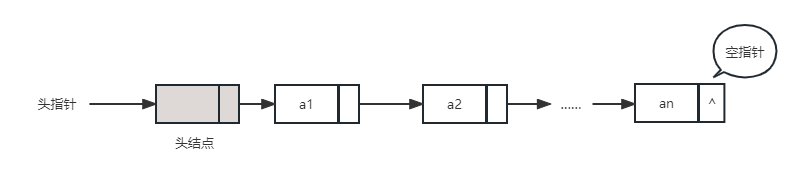
• 在表示的时候，可能有头结点，也可能没有
  • 有头结点时，该结点中指针域的指针指向第一个元素结点，并令头指针指向头结点

• 结构表示

  C

  typedef struct LNode{
      ElemType data;
      struct LNode* next;
  }LNode,*Linklist;
  

• 基本操作

  初始化销毁结构查找元素插入元素删除元素求表长建立单链表判空

  • 时间复杂度为 \(O(1)\)
    C++

    void InitList(LinkList &L)
    {
        // 创建一个带头结点的空链表，L 为指向头结点的指针
        L = new LNode;
        if (!L) exit(1); // 存储空间分配失败
        L->next = NULL;
    } // InitList
    

  • 时间复杂度为 \(O(Listlength(L))\)
    C++

    void DestroyList(LinkList &L)
    {
        // 销毁以L为头指针的单链表，释放链表中所有结点空间
        LinkList p = L;
        while(p)
        {
            pTemp = p;
            p = p->next;
            delete pTemp;
        } // while
        L = NULL;
    } // DestroyList
    

  • 时间复杂度为 \(O(Listlength(L))\)

  按值查找LocateElem(L,e,compare())按位查找GetElem(L,i,&e)

  C++

  int LocateElem(LinkList L, ElemType e, int (*compare)(ElemType, ElemType)) {
      //在线性表L中查找第1个值与e满足compare()的元素的位序。若找到，则返回其在L中的位序，否则返回-1。
      int pos = 0;
      LNode *p = L->next;
      while (p) {
          if ((*compare)(e,p->data)) {
              return pos;
          } else {
              pos++;
              p = p->next;
          }
      }
      return -1;
  } // LocateElem
  

  C++

  bool GetElem (LinkList L， int pos， ElemType &e){
  // 若1≤pos≤LengthList(L)，则用 e 带回指针L指向头结点的单链表中第 pos 个元素的值且返回函数值为TRUE,否则返回函数值为FALSE
      p = L->next; j =1; // 变量初始化，p 指向第一个结点
      while ( p && j< pos )
      {
          // 顺结点的指针向后查找，直至 p 指到第pos个结点或 p 为空止
          p = p->next; ++j;
      } // while
      if ( !p || j>pos ) return FALSE; // 链表中不存在第 pos 个结点
      e = p->data; // 取到第 pos 个元素
      return TRUE;
  } // GetElem
  

  指定位置插入ListInsert(&L,pos,e)指定结点后插InsertNext(p,e)指定结点前插InsertPriorNode(&L,p,e)

  • 时间复杂度为 \(O(ListLength(L))\)

  C++

  bool ListInsert(LinkList &L，int pos，ElemType e)
  {
      // 若1≤pos≤LengthList(L)+1，则在指针L指向头结点的单链表的第 pos 个元素之前插入新的元素 e，且返回函数值为 TRUE，否则不进行插入且返回函数值为 FALSE
      p=L; j=0;
      while(p && j<pos-1)
      { // 查找第pos-1个结点，并令指针p指向该结点
          p=p->next;++j;
      } // while
      if (!p||j>pos-1) return FALSE; // 参数不合法
      LNode s=new LNode;
      if (!s) exit(1); // 存储空间分配失败
      s->data=e; // 创建新元素的结点
      s->next=p->next; p->next=s; // 修改指针
      return TRUE；
  } // ListInsert
  

  • 时间复杂度为 \(O(1)\)

  C++

  bool InsertNext(LNode p, ElemType e)
  {
      // 在结点p的后继插入以e为数据的节点
      if(p==NULL) return false;
      LNode s = new LNode;
      if(!s) return false;
      s->next = p->next;
      s->data = e;
      p->next = s;
      return true;
  }
  

  • 时间复杂度为 \(O(ListLength(L))\)

  有表头参数无表头参数

  C++

  bool InsertPriorNode(LinkList &L,LNode p,ElemType e)
  {
      //在结点p的前驱插入元素e
      if(p==NULL) return false;
      LNode q = L;
      while(q->next!==p) q = q->next;
      q->data = e;
      LNode s = new LNode;
      if(!s) return false;
      s->next = p;
      q->next = s;
      return true;
  }
  

  C++

  bool InsertPriorNode(LNode p,LNode s)
  {
      // 在结点p的前驱插入结点s
      if(p==NULL||s==NULL) return false;
      s->next = p->next;
      p->next = s;
      ELemType temp = p->data;
      p->data = s->data;
      s->data = temp;
      return true;
  }
  

  • 时间复杂度为 \(O(ListLength(L))\)

  指定位置删除ListDelete(&L,i,&e)指定节点删除DeleteNode(&L,p,&e)

  C++

  bool ListDelete(LinkList &L， int pos， ElemType &e)
  {
      // 若1≤pos≤LengthList(L)，则删除指针L指向头结点的单链表中第 pos 个元素并以 e 带回其值，返回函数值为 TRUE，否则不进行删除操作且返回函数值为 FALSE
      p = L; j = 0;
      while (p->next && j < i-1)
      {p = p->next; ++j;} // 寻找第pos个结点，并令p指向其前驱
      if (!(p->next) || j > i-1)
      return FALSE; // 删除位置不合理
      q = p->next; p->next = q->next; // 修改指针
      e = q->data; delete(q); // 释放结点空间
      return TRUE;
  } // ListDelete
  

  C++

  bool DeleteNode(LinkList &L, LNode p,ElemType &e)
  {
      e = p->data;
      if(p->next!=NULL){
          LNode q = p->next;
          p->data = p->next->data;
          p->next = q->next;
          delete q;
      }
      else{
          LNode temp = L;
          while(temp->next!=p) temp = temp->next;
          temp->next = NULL;
          delete p;
      }
      return TRUE;
  }
  

  C++

  int length(LinkList L)
  {
      int len = 0;
      LNode *p = L->next;
      while(p->next){
          len++;
          p = p->next;
      }
  }
  

  头插法尾插法

  • 在链表的开头插入一个新的节点，也就是，必须使得链表头Head指向新节点，该新节点指向原来是表头的第一个节点。
  • 生成的链表是逆序的

  C++

  void createList(LinkList &L,ElemType[] datas)
  {
      L = new LNode;
      if(!L) exit(1);
      L->next = NULL;
      int n = datas.length();
      for(int i = n; i > 0 ;--i){
          LNode p = new LNode;
          if(!p) exit(1);
          p->data = datas[i-1];
          p->next = L->next;
          L->next = p;
      }
  }
  

  • 在链表的尾部插入一个节点。尾插法生成一个新节点后直接插入链表的微端，也就是让原来最后一个节点指向该新节点。
  • 生成的链表是顺序的

  C++

  void createList(LinkList &L,ElemType[] datas)
  {
      L = new LNode;
      if(!L) exit(1);
      L->next = NULL;
      LNode r = L;
      int n = datas.length();
      for(int i = 0; i < n ;i++){
          LNode p = new LNode;
          if(!p) exit(1);
          p->data = datas[i];
          r->next = p;
          r = r->next;
      }
      r->next = NULL;
  }
  

  带头结点的单链表不带头结点的单链表

  C++

  bool isEmpty(LinkList L){
      return L->next==NULL;
  }
  

  C++

  bool isEmpty(LinkList L){
      return L==NULL;
  }
  

静态链表

• 用数组描述的链表结构，数组的第零分量表示头结点，每个结点的指针域表示下一结点在数组中的相对位置
• 结构表示
  C

  #define MAXSIZE 100;
  typedef struct{
      ElemType data；
      int cur；
  }elem,SLinkList[MAXSIZE];
  

循环链表

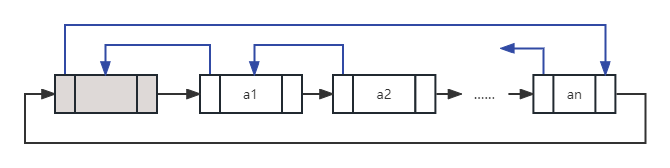
循环链表

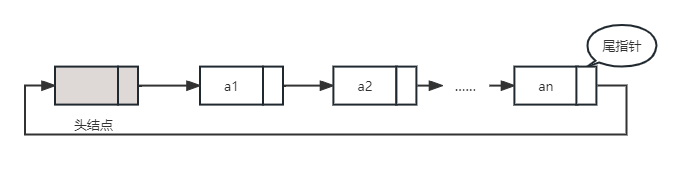
• 表中最后一个结点的指针域指向头结点，整个链表成为一个由链指针相链接的环，并且设立尾指针设成指向最后一个结点。
• 空的循环链表由只含一个自成循环的头结点表示。

• 循环单链表的判空：L->next==L
• 是否为循环单链表的尾结点：p->next==L

双链表

双链表

• 双向链表也是由指向头结点的头指针唯一确定，若将头尾结点链接起来则构成双向循环链表
• 其结点结构中含有两个指针域，其一指向数据元素的“直接后继”，另一指向数据元素的“直接前驱”
• 结构表示
  C

  typdef struct DNode{
      ElemType data;
      struct DNode *prior, *next;
  }DNode*,DLinkList
  

• 双链表的插入操作
  C++

  void insertNext(DNode p,DNode s)
  {
      // 在p结点之后插入结点s
      s->next = p->next;
      p->next = s;
      s->next->prior = s;
      s->prior = p;
  }
  

• 双链表的删除操作
  C++

  void deleteNode(DNode p,ELemType &e)
  {
      // 删除结点p的后继，用e返回数据元素
      DNode q = p->next;
      e = q->data;
      p->next = q->next;
      p->next->prior = p;
      delete q;
  }
  

顺序表 vs 链表 总结

	顺序表	链表
逻辑结构	线性结构	线性结构
存储结构	顺序存储（随机存取）	随机存储
操作-创建	需要预分配连续空间	仅分配头结点
操作-销毁	系统回收（静态分配） 手动释放（动态分配）	依次释放掉每一个节点
操作-增删	其他元素依次前移/后移 复杂度 \(O(n)\)	修改指针 复杂度 \(O(n)\)
操作-查找	按位：\(O(1)\) 按值：\(O(n)\) (若有序，可以达到 \(O(log_2n)\) )	按位： \(O(n)\) 按值：\(O(n)\)
特点	存储密度高	改变容量方便

评论